機器學習必知概念：貝葉斯估計、最大似然估計、最大後驗估計

原文(個人博客):貝葉斯估計、最大似然估計、最大後驗估計三者的區別

更多機器學習深度學習資源

---

實例分析

即便學過機器學習的人，對機器學習中的 MLE(極大似然估計)、MAP(最大後驗估計)以及貝葉斯估計(Bayesian) 仍有可能只知其一;不知其二。對於一個基礎模型，一般均可以從這三個角度去建模，好比對於邏輯迴歸（Logistics Regression）來講：

MLE: Logistics Regression

MAP: Regularized Logistics Regression
Bayesian: Bayesian Logistic Regression

本文結合實際例子，以通俗易懂的方式去講解這三者之間的本質區別，但願幫助讀者掃清理解中的障礙。

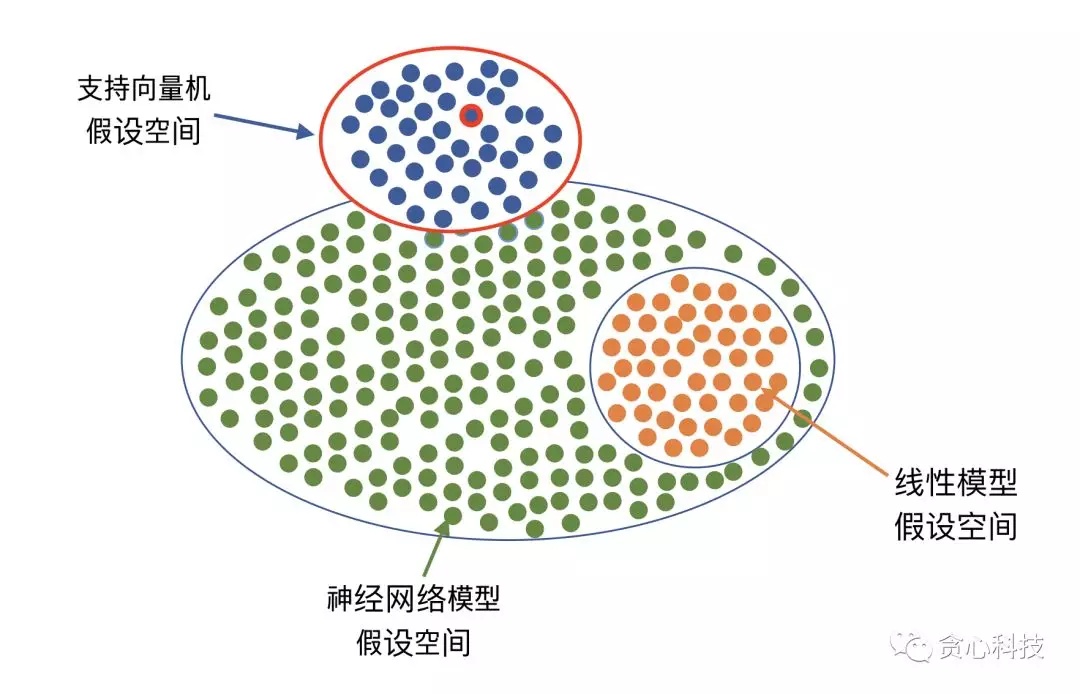
先導知識點： 假設空間（Hypothesis Space）

什麼叫假設空間呢？咱們能夠這樣理解。機器學習包含不少種算法，好比線性迴歸、支持向量機、神經網絡、決策樹、GDBT等等。咱們在建模的時候，第一步就是要選擇一個特定的算法好比「支持向量機」。**一旦選擇了一個算法，就至關於咱們選擇了一個假設空間。**在一個假設空間裏，咱們一般會有無數種不一樣的解（或者能夠理解成模型），一個優化算法（好比梯度降低法）作的事情就是從中選擇最好的一個解或者多個解/模型，固然優化過程要依賴於樣本數據。舉個例子，若是咱們選擇用支持向量機，那至關於咱們可選的解/模型集中在上半部分（藍色點）。

一個具體「toy」問題

「 張三遇到了一個數學難題，想尋求別人幫助。經過一番思考以後發現本身的朋友在清華計算機系當老師。因而，他決定找清華計算機系學生幫忙。那張三用什麼樣的策略去尋求幫助呢？

在這裏，「清華計算機系」是一個假設空間。在這個假設空間裏，每一位學生能夠看作是一個模型（的實例化）。

對於張三來講，他有三種不一樣的策略能夠選擇。

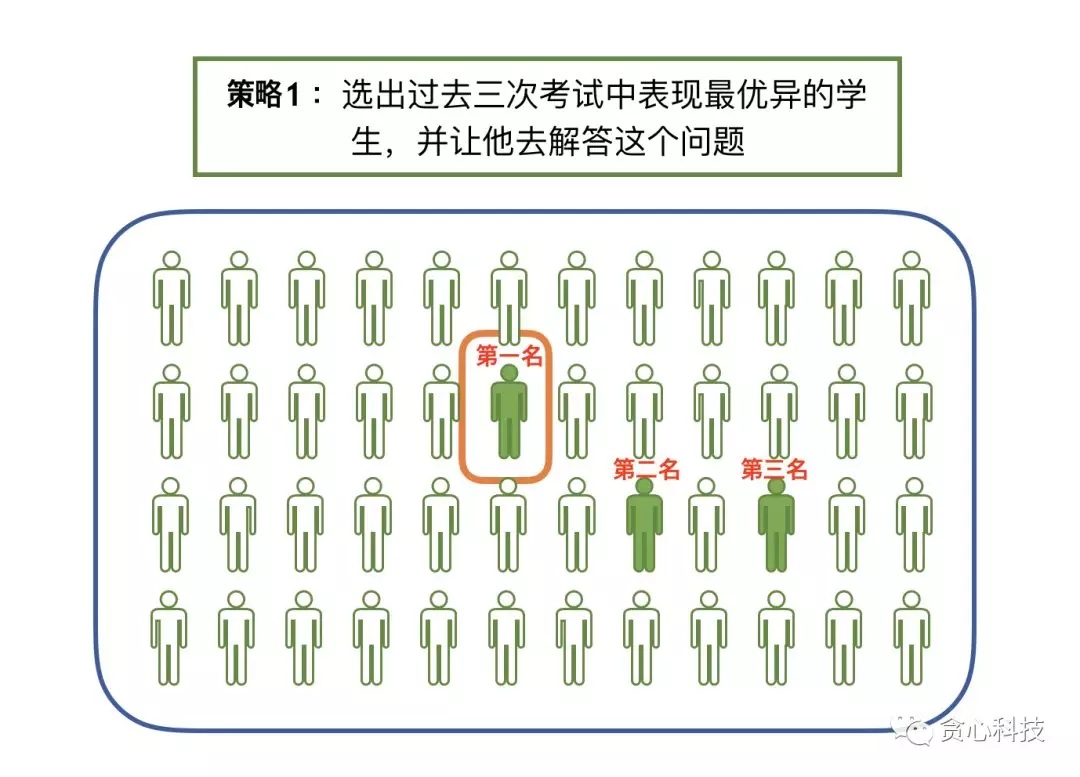
第一種策略 : MLE

第一種策略就是從系裏選出過往成績最好的學生，並讓他去解答這個難題。好比咱們能夠選擇過去三次考試中成績最優秀的學生。

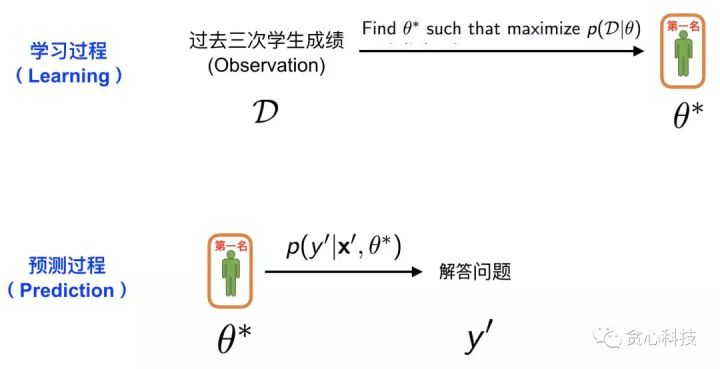
**通常的學習流程分爲「學習過程」和「預測過程」。第一種策略的方案能夠用下面的圖來表示。**在這裏，學習過程至關於從全部系的學生中挑選出成績最好的學生。因此，這裏的「學生過往成績單」就是咱們已知的訓練數據 D， 選出成績最好的學生（計算曆史平均分數，並選出最高的），這個過程就是MLE。一旦咱們找到了成績最好的學生，就能夠進入預測環節。在預測環節中，咱們就可讓他回答張三手裏的難題 x', 以後就能夠獲得他給出的解答 y'。

第二種策略：MAP

跟第一種策略的不一樣點在於，第二種策略中咱們聽取了老師的建議，老師就是張三的朋友。這位老師給出了本身的觀點：_「小明和小花的成績中可能存在一些水分」。_當咱們按照成績的高低給學生排序，假設前兩名依次爲小明和小花，若是咱們不考慮這位老師的評價，則咱們確定把小明做爲目標對象。然而，既然老師已經對小明和小花作了一些負面的評價，那這個時候，咱們頗有可能最後選擇的是班級裏的第三名，而不是小明或者小花。

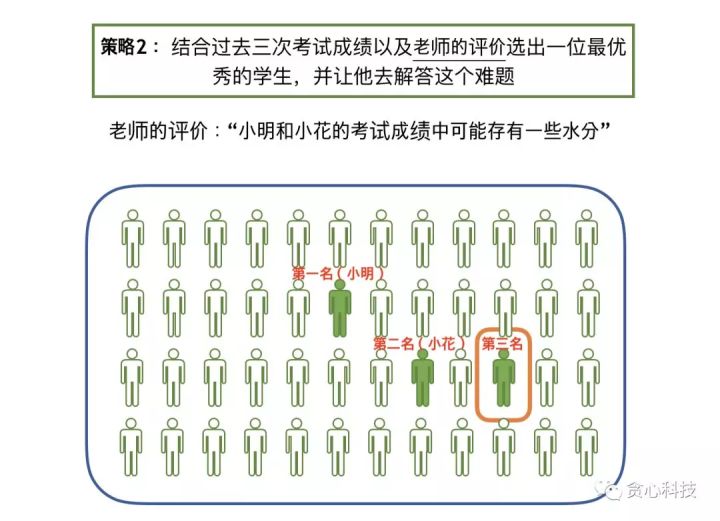
咱們把第二種策略的過程也用一個圖來描述。與上面的圖相比，惟一的區別在於這裏多出了老師的評價，咱們稱之爲 Prior。 也就是說咱們根據學生以往的成績並結合老師評價，選擇了一位咱們認爲最優秀的學生（能夠當作是模型）。以後就可讓他去回答張老師的難題 x'，並獲得他的解答 y'。整個過程相似於MAP的估計以及預測。

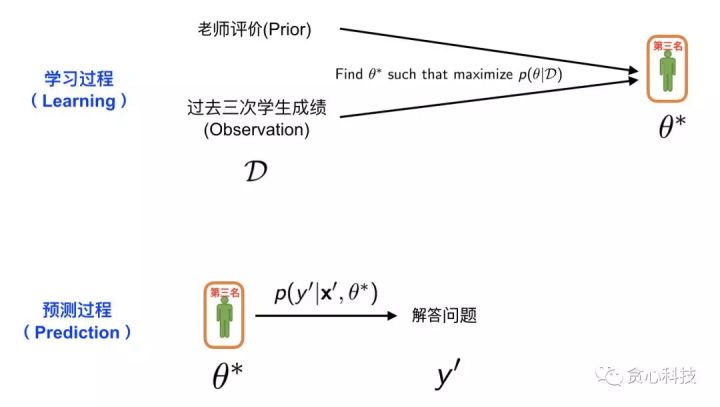
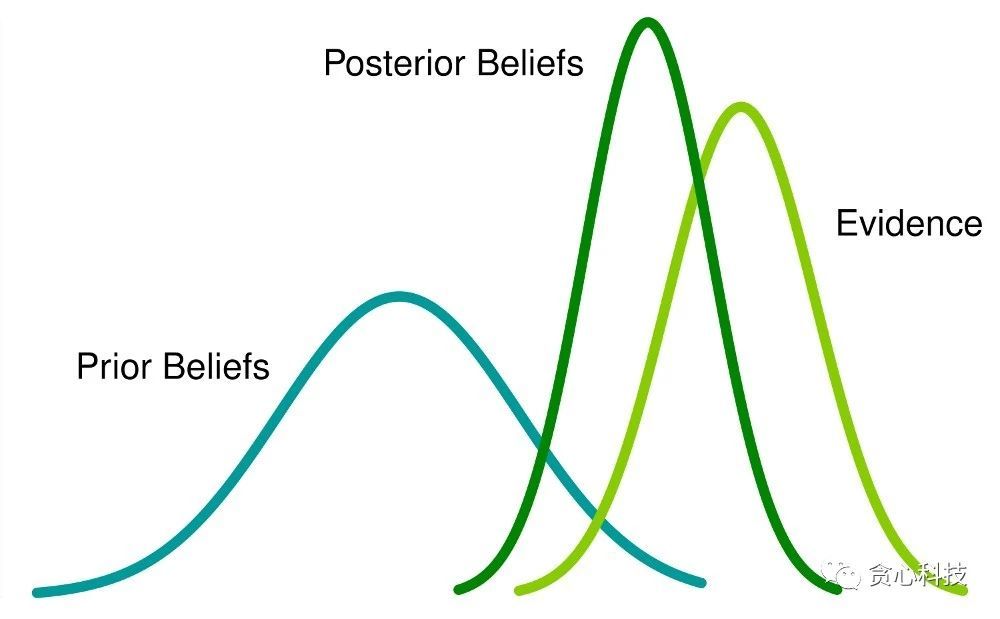
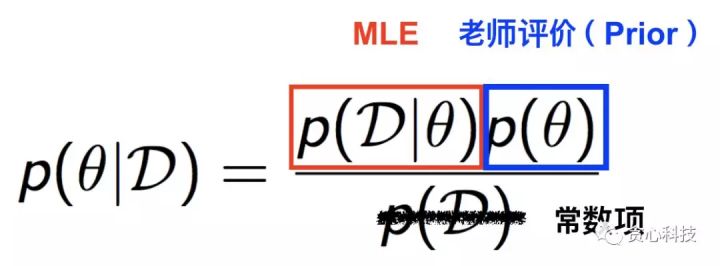
到這裏，有些讀者可能會有一些疑惑：「老師的評價(Prior)跟學生過往的成績（Observation）是怎麼結合在一塊兒的？」。 爲了回答這個問題，咱們不得不引出一個很是著名的定理，叫作**貝葉斯定理，**以下圖所示。左邊的項是MAP須要優化的部分，經過貝葉斯定理這個項能夠分解成MLE（第一種策略）和Prior，也就是老師的評價。在這裏，分母是常數項（Constant），因此不用考慮。

第三種策略 - Bayesian

最後，咱們來介紹第三種策略。這種策略應該不少人也能夠想象獲得，**其實就是讓全部人都去參與回答張三的難題，但最後咱們經過一些加權平均的方式得到最終的答案。**好比有三個學生，並且咱們對這三個學生狀況沒有任何瞭解。經過提問，第一個學生回答的答案是A，第二個學生回答的答案也是A，但第三個學生回答的是B。在這種狀況下，咱們基本能夠把A做爲標準答案。接着再考慮一個稍微複雜的狀況，假設咱們經過以往他們的表現得知第三個學生曾經屢次得到過全國奧賽的金牌，那這個時候該怎麼辦？ 很顯然，在這種狀況下，咱們給予第三個學生的話語權確定要高於其餘兩位學生。

咱們把上面的這種思路應用到張三的問題上，其實至關於咱們讓全部計算機系的學生參與回答這個問題，以後把他們的答案進行彙總並得出最終的答案。若是咱們知道每一位學生的話語權（權重），這個彙總的過程是肯定性（deterministic)。 但每一位學生的話語權（權重）怎麼獲得呢？ 這就是貝葉斯估計作的事情！

咱們用下面的一幅圖來說述貝葉斯估計和預測的整個過程。跟MAP相似，咱們已知每一位學生過去三次考試考試成績（D）以及老師的評價（Prior）。 但跟MAP不一樣的是，**咱們這裏的目標再也不是- 「選出最優秀的學生」，而是經過觀測數據（D）去得到每一位學生的發言權（權重），**並且這些權重所有加起來要等於1， 至關因而一個valid分佈(distribution)。

總結起來，在第三種策略之下，給定過去考試成績(D)和老師的評價（Prior）, 咱們的目標是估計學生權重的分佈，也稱之爲Posterior Distribution。 那這個分佈具體怎麼去估計呢？ 這部分就是貝葉斯估計作的事情，有不少種方法能夠作這件事情，好比MCMC, Variational Method等等，但這並非本文章的重點，因此不在這裏進一步解釋，有興趣的讀者能夠關注以後關於貝葉斯的專欄文章。從直觀的角度思考，由於咱們知道每一位學生過往的成績，因此咱們很容易瞭解到他們的能力水平進而估計出每一位學生的話語權（權重）。

一旦咱們得到了這個分佈（也就是每一位學生的權重），接下來就能夠經過相似於加權平均的方式作預測了，那些權重高的學生話語權天然就越大。

以上是對MLE, MAP以及貝葉斯估計的基本講解。下面咱們試圖去回答兩個常見的問題。

Q: 隨着咱們觀測到愈來愈多的數據，MAP估計逐步逼近MLE，這句話怎麼理解？

咱們接着使用以前MAP（第二種策略）的例子。在這裏，咱們對原來的問題稍做改變。在以前的例子裏咱們假設可以獲得每一位學生過去三次考試中的成績。但在這裏，咱們進一步假定能夠得到每一位學生過去100次考試中的成績。

那這樣的修改會帶來什麼樣的變化呢？ 若是仔細想想，其實也很容易想獲得。咱們設想一下這樣的兩種場景。假設咱們知道某一位學生過去三次的考試成績比較優異，但老師卻告訴咱們這位學生能力其實不怎麼樣，那這時候咱們極可能就去相信老師了，畢竟僅僅經過三次考試的成績很難對一個學生有全面的瞭解。但相反，假設咱們瞭解到這位學生在過去100次考試中所有得到了班裏第一名，但同時老師又告訴咱們這位學生的能力其實不怎麼樣，那這時候咱們會有什麼樣的反應？ 兩三次考試或許能夠算作是運氣，但連續100次都是第一名這件事情很難再跟運氣畫等號吧？ 咱們甚至可能會去懷疑老師的品德，是否是故意污衊人家？

這就是說，當咱們觀測到的數據愈來愈多的時候，咱們從數據中獲取的信息的置信度是越高的，相反老師提供的反饋（Prior）的重要性就會逐漸下降。理想狀況下，當咱們擁有無窮多的數據樣本時，MAP會逼近MLE估計，道理都是同樣的。

Q: 爲何貝葉斯估計會比MLE, MAP難？

回顧一下，MLE 和MAP都是在尋找一個最優秀的學生。貝葉斯估計則是在估計每一位學生的權重。第一種狀況下，爲了尋找最優秀的學生，咱們只需知道學生之間的「相對」優秀程度。這個怎麼理解呢？ 好比一個班裏有三個學生A,B,C，咱們知道學生A比B優秀，同時知道B比C優秀，那這時候就能夠推斷出學生A是最優秀的，咱們並不須要明確知道A的成績是多少，B的成績是多少.....

但在貝葉斯估計模式下，咱們必需要知道每個學生的絕對權重，由於最後咱們得到的答案是全部學生給出的答案的加權平均，並且全部學生的權重加起來要保證等於1(任何一個分佈的積分和必需要等於1）。 假設咱們知道每一位學生的能力值，a1, a2,.... an，這個能做爲權重嗎？ 顯然不能。爲了得到權重，有一種最簡單的方法就是先求和，而後再求權重。好比先計算 a1+...+an = S, 再用a1/S 做爲權重。這貌似看起來也不難啊，只不過多作了一個加法操做？

咱們很容易看出這個加法操做的時間複雜度是O(n)，依賴於整體學生的數量。若是咱們的假設空間只有幾百名學生，這個是不成問題的。 但實際中，好比咱們假設咱們的模型用的是支持向量機，而後把假設空間裏的每個可行解比喻成學生，那這個假設空間裏有多少個學生呢？ 是無數個！！， 也就是說須要對無窮多個數作這種加法操做。 固然，這種加法操做會以積分(integeral)的方式存在，但問題是這種積分一般沒有一個closed-form的解，你必需要去近似地估計才能夠，這就是MCMC或者Variational方法作的事情，不在這裏多作解釋。

本文幾點重要的Take-aways：

• 每個模型定義了一個假設空間，通常假設空間都包含無窮的可行解；
• MLE不考慮先驗（prior)，MAP和貝葉斯估計則考慮先驗（prior）；
• MLE、MAP是選擇相對最好的一個模型（point estimation）， 貝葉斯方法則是經過觀測數據來估計後驗分佈(posterior distribution)，並經過後驗分佈作羣體決策，因此後者的目標並非在去選擇某一個最好的模型；
• 當樣本個數無窮多的時候，MAP理論上會逼近MLE；
• 貝葉斯估計複雜度大，一般用MCMC等近似算法來近似；

最後貼一張總結的圖:

---

理論分析

一。機器學習

  核心思想是從past experience中學習出規則，從而對新的事物進行預測。對於監督學習來講，有用的樣本數目越多，訓練越準確。

用下圖來表示機器學習的過程及包含的知識：

簡單來講就是：

1. 首先要定義咱們的假設空間（Model assumption）：如線性分類，線性迴歸，邏輯迴歸，SVM，深度學習網絡等。
2. 如何衡量咱們學出來的模型的好壞？定義損失函數（目標函數），lost function，如square loss
3. 如何對假設的模型作優化，及optimization過程。簡單說，就是選擇一種算法（如：梯度降低，牛頓法等），對目標函數進行優化，最終獲得最優解；
   1. 不一樣的模型使用不一樣的算法，如邏輯迴歸一般用梯度降低法解決，神經網絡用反向推導解決，貝葉斯模型則用MCMC來解決。
   2. 機器學習 = 模型 + 優化（不一樣算法）
4. 還有一個問題，模型的複雜度怎麼衡量？由於複雜的模型容易出現過擬合（overfitting）。解決過擬合的方就是加入正則項（regularization）
5. 以上問題都解決以後，咱們怎麼判斷這個解就是真的好的呢？用**交叉驗證（cross-validation）**來驗證一下。

二。ML vs MAP vs Bayesian

1. ML（最大似然估計）：就是給定一個模型的參數，而後試着最大化p(D|參數)。即給定參數的狀況下，看到樣本集的機率。目標是找到使前面機率最大的參數。
   1. 邏輯迴歸都是基於ML作的；
   2. 缺點：不會把咱們的先驗知識加入模型中。
2. MAP（最大後驗估計）：最大化p(參數|D)。
3. Bayesian：咱們的預測是考慮了全部可能的參數，即全部的參數空間（參數的分佈）。

• ML和MAP都屬於同一個範疇，稱爲（freqentist），最後的目標都是同樣的：找到一個最優解，而後用最優解作預測。

三。ML

咱們須要去最大化p(D|參數)，這部分優化咱們一般能夠用把導數設置爲0的方式去獲得。然而，ML估計不會把先驗知識考慮進去，並且很容易形成過擬合現象。

舉個例子，好比對癌症的估計，一個醫生一天可能接到了100名患者，但最終被診斷出癌症的患者爲5我的，在ML估計的模式下咱們獲得的獲得癌症的機率爲0.05。

這顯然是不太切合實際的，由於咱們根據已有的經驗，咱們知道這種機率會低不少。然而ML估計並無把這種知識融入到模型裏。

四。MAP

經過上面的推導咱們能夠發現，MAP與ML最大的不一樣在於p(參數)項，因此能夠說MAP是正好能夠解決ML缺少先驗知識的缺點，將先驗知識加入後，優化損失函數。

其實p(參數)項正好起到了正則化的做用。如：若是假設p(參數)服從高斯分佈，則至關於加了一個L2 norm；若是假設p(參數)服從拉普拉斯分佈，則至關於加了一個L1 norm。

五。Bayesian

再次強調一下： ML和MAP只會給出一個最優的解， 然而貝葉斯模型會給出對參數的一個分佈，好比對模型的參數, 假定參數空間裏有參數1,參數2, 參數3,...參數N，貝葉斯模型學出來的就是這些參數的重要性（也就是分佈），而後當咱們對新的樣本預測的時候，就會讓全部的模型一塊兒去預測，但每一個模型會有本身的權重（權重就是學出來的分佈）。最終的決策由全部的估計根據其權重作出決策。

模型的ensemble的卻大的優勢爲它能夠reduce variance, 這根投資很相似，好比咱們投資多種不一樣類型的股票，總比投資某一個股票時的風險會低。

六。上面提到了frequentist和bayesian，二者之間的區別是什麼？

用一個簡答的例子來再總結一下。 好比你是班裏的班長，你有個問題想知道答案，你能夠問全部的班裏的學生。 一種方案是，問一個學習最好的同窗。 另外一種方案是，問全部的同窗，而後把答案綜合起來，但綜合的時候，會按照每一個同窗的成績好壞來作個權重。 第一種方案的思想相似於ML,MAP，第二種方案相似於貝葉斯模型。

七。Bayesian的難點

因此整個貝葉斯領域的核心技術就是要近似的計算 p(\theta|D），咱們稱之爲bayesian inference,說白了，這裏的核心問題就是要近似這個複雜的積分（integral), 一種解決方案就是使用蒙特卡洛算法。好比我想計算一個公司全部員工的平均身高，這個時候最簡答粗暴的方法就是讓行政去一個一個去測量，而後計算平均值。但想計算全部中國人的平均身高，怎麼作？（顯然一個個測量是不可能的）

即採樣。咱們隨機的選取一些人測量他們的身高，而後根據他們的身高來估計全國人民的審稿。固然採樣的數目越多越準確，採樣的數據越有表明性越準確。這就是蒙特卡洛算法的管家思想。

再例：

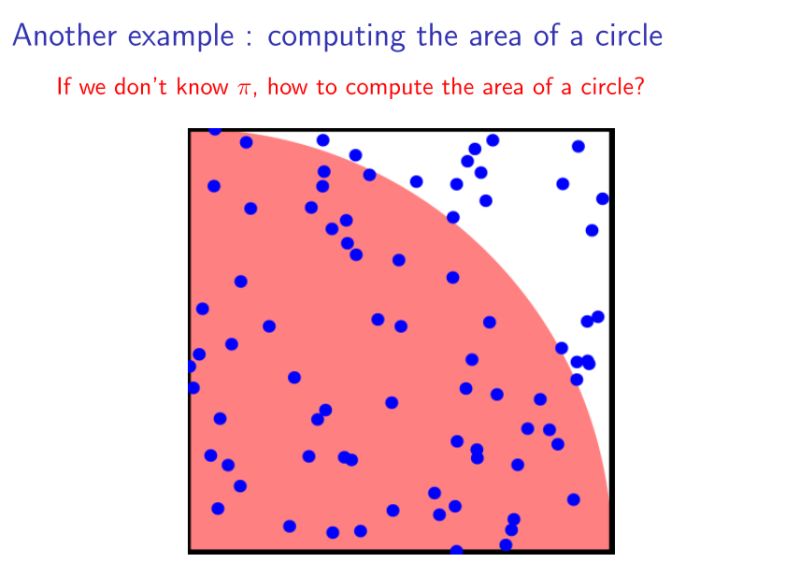
假設咱們不知道π，可是想計算圓的面積。也能夠經過採樣的方法近似獲得。隨機再下圖所示的正方形中撒入一些點，記落入紅色區域的點的個數爲n1,落入白色區域的個數爲n2，則四分之一圓的面積就爲n1/(n1+n2).——蒙特卡洛思想

那麼，如何對連續函數估計呢？採樣n多個數據，逼近最後的積分值。

假設咱們要計算 f(x)的指望值， 咱們也有p(x)這種分佈，這個時候咱們就能夠不斷的從p(x)這個分佈裏作一些採樣，好比 x1,x2,...xn, 而後用這些採樣的值去算f(x),  因此最後獲得的結果就是 (f(x1) + f(x2),, + f(xn))/ n

然鵝，上面例子中提到的採樣都是獨立的。也就是每一個樣本跟其餘的樣本都是獨立的，不影響彼此之間的採樣。然而，在現實問題上，有些時候咱們想加快有效樣本的採樣速度。這個問題討論的就是怎麼優化採樣過程了，也是機器學習裏一個比較大的話題了。

重申一下，用上面提到的採樣方式咱們能夠去近似估計複雜的積分，也能夠計算圓的面積，也能夠計算全國人口的平均身高。但這個採樣方式是獨立的，有些時候，咱們但願咱們用更少的樣本去更準確的近似某一個目標，因此就出現了sampling這種一個領域的研究，就是在研究以什麼樣的方式優化整個採樣過程，使得過程更加高效。

MCMC這種採樣方法，全稱爲markov chain monte carlo採樣方法，就是每一個採樣的樣本都是互相有關聯性的。

可是MCMC算法須要在整個數據集上計算。也就是說爲了獲得一個樣本，須要用全部的數據作迭代。這樣當N很大時，顯然不適用。並且限制了貝葉斯方法發展的主要緣由就是計算複雜度過高。所以如今貝爺第領域人們最關心的問題是：怎麼去優化採樣，讓它可以在大數據環境下學習出貝葉斯模型？

下降迭代複雜度的一個實例：

對於邏輯迴歸，使用梯度降低法更新參數時，有批量梯度降低法（即便用整個數據集去更新參數），爲了下降計算複雜度，人們使用了隨機梯度降低法，即隨機從數據集中選取樣原本更新參數。

因此，可否將此思想用於MCMC採樣中呢？

Yes！langevin dynamic（MCMC算法中的一種），和stochastic optimizaiton(好比隨機梯度降低法)能夠結合在一塊兒用。這樣，咱們就能夠經過少許的樣本去作採樣，這個時候採樣的效率就不在依賴於N了，而是依賴於m, m是遠遠小於N。

---

參考文獻

[1] 貪心科技. 機器學習中的MLE、MAP和貝葉斯估計[DB/OL]. https://zhuanlan.zhihu.com/p/37543542, 2018-06-20.

[2] 江湖小妞. 貝葉斯思想以及與最大似然估計、最大後驗估計的區別[DB/OL]. http://www.cnblogs.com/little-YTMM/p/5399532.html, 2018-06-20.