TensorFlow實戰之K-Means聚類算法實踐

原文地址：這裏

Google 最近開源了它的第二代人工智能與數值計算庫TensorFlow。TensorFlow由Google大腦團隊開發，而且可以靈活地運行在多個平臺上——包括GPU平臺與移動設備中。

TensorFlow的核心就是使用所謂的數據流，能夠參考Wikipedia上的有關於Genetic Programming 的相關知識，譬如：

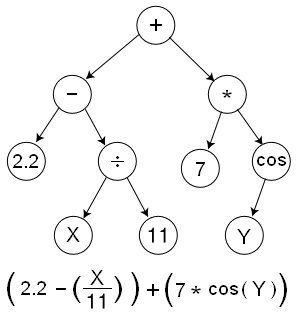
正如你理解的，整個以樹狀圖的架構來表示整個計算流。每一個節點即表明一個操做，TensorFlow稱做OPS，即operations的縮寫。非葉子節點仍是很好理解的，一些葉子節點能夠是特殊的操做類型，譬如返回一個常量值(譬如上述樹中的7或者2.2)。其餘的一些葉子節點，譬如X或者Y這樣的，被當作placeholders，即會在運行中被動態地注入值。若是仔細觀察上圖中的箭頭的指向，能夠發現這些箭頭指向就代表了不一樣節點之間輸出的依賴關係。所以，Data(在TensorFlow中被稱爲Tensors)，會在不一樣的節點之間逆向流動，這就就是他們被稱爲TensorFlow的緣由。TensorFlow也提供了其餘的基於圖像抽象的組件，譬如持久化的數據存儲(被稱爲Variables)，以及在譬如神經網絡這樣的應用中對於Variables中的參數微調而進行的優化手段。

TensorFlow提供了很是有好的Python的接口，在看本篇文章以前建議閱讀如下：

1.基礎環境的搭建或者筆者的翻譯

2.參閱這個例子 來對TensorFlow的代碼風格有一個模糊的認識。

3.接下來這個解釋 會闡述TensorFlow中的基礎的組件。

4.參考詳細的例子 來看看TensorFlow是怎麼解決常見的ML問題的。

5.在瞭解上述的基本知識後，能夠閱讀Python docs這個接口文檔來做爲開發中的參考。

接下來，我會以用TensorFlow來解決常見的K-Means問題做爲例子來闡述如何使用它。

import tensorflow as tf
from random import choice, shuffle
from numpy import array
 
 
def TFKMeansCluster(vectors, noofclusters):
    """
    K-Means Clustering using TensorFlow.
    `vertors`應該是一個n*k的二維的NumPy的數組，其中n表明着K維向量的數目
    'noofclusters' 表明了待分的集羣的數目，是一個整型值
    """
 
    noofclusters = int(noofclusters)
    assert noofclusters < len(vectors)
 
    #找出每一個向量的維度
    dim = len(vectors[0])

    #輔助隨機地從可得的向量中選取中心點
    vector_indices = list(range(len(vectors)))
    shuffle(vector_indices)
 
    #計算圖
    #咱們建立了一個默認的計算流的圖用於整個算法中，這樣就保證了當函數被屢次調用      #時，默認的圖並不會被從上一次調用時留下的未使用的OPS或者Variables擠滿
 
    graph = tf.Graph()
 
    with graph.as_default():
 
        #計算的會話
 
        sess = tf.Session()
 
        ##構建基本的計算的元素
         
        ##首先咱們須要保證每一箇中心點都會存在一個Variable矩陣
        ##從現有的點集合中抽取出一部分做爲默認的中心點
        centroids = [tf.Variable((vectors[vector_indices[i]]))
                     for i in range(noofclusters)]
        
        ##建立一個placeholder用於存放各個中心點可能的分類的狀況
        centroid_value = tf.placeholder("float64", [dim])
        cent_assigns = []
        for centroid in centroids:
            cent_assigns.append(tf.assign(centroid, centroid_value))
 
        ##對於每一個獨立向量的分屬的類別設置爲默認值0
        assignments = [tf.Variable(0) for i in range(len(vectors))]
        
        ##這些節點在後續的操做中會被分配到合適的值
        assignment_value = tf.placeholder("int32")
        cluster_assigns = []
        for assignment in assignments:
            cluster_assigns.append(tf.assign(assignment,
                                             assignment_value))
 
        ##下面建立用於計算平均值的操做節點
        #輸入的placeholder
        mean_input = tf.placeholder("float", [None, dim])
        
        #節點/OP接受輸入，而且計算0維度的平均值，譬如輸入的向量列表
        mean_op = tf.reduce_mean(mean_input, 0)
 
        ##用於計算歐幾里得距離的節點
        v1 = tf.placeholder("float", [dim])
        v2 = tf.placeholder("float", [dim])
        euclid_dist = tf.sqrt(tf.reduce_sum(tf.pow(tf.sub(
            v1, v2), 2)))
 
        ##這個OP會決定應該將向量歸屬到哪一個節點
        ##基於向量到中心點的歐幾里得距離
        #Placeholder for input
        centroid_distances = tf.placeholder("float", [noofclusters])
        cluster_assignment = tf.argmin(centroid_distances, 0)
 
        ##初始化全部的狀態值
         ##這會幫助初始化圖中定義的全部Variables。Variable-initializer應該定         ##義在全部的Variables被構造以後，這樣全部的Variables纔會被歸入初始化
        init_op = tf.initialize_all_variables()
 
        #初始化全部的變量
        sess.run(init_op)
 
        ##集羣遍歷
         
        #接下來在K-Means聚類迭代中使用最大指望算法。爲了簡單起見，只讓它執行固           #定的次數，而不設置一個終止條件
        noofiterations = 100
        for iteration_n in range(noofiterations):
 
            ##指望步驟
            ##基於上次迭代後算出的中心點的未知
            ##the _expected_ centroid assignments.
            #首先遍歷全部的向量
            for vector_n in range(len(vectors)):
                vect = vectors[vector_n]
                
                #計算給定向量與分配的中心節點之間的歐幾里得距離
                distances = [sess.run(euclid_dist, feed_dict={
                    v1: vect, v2: sess.run(centroid)})
                             for centroid in centroids]
                #下面能夠使用集羣分配操做，將上述的距離當作輸入
                assignment = sess.run(cluster_assignment, feed_dict = {
                    centroid_distances: distances})
                #接下來爲每一個向量分配合適的值
                sess.run(cluster_assigns[vector_n], feed_dict={
                    assignment_value: assignment})
 
            ##最大化的步驟
            #基於上述的指望步驟，計算每一個新的中心點的距離從而使集羣內的平方和最小
            for cluster_n in range(noofclusters):
                #收集全部分配給該集羣的向量
                assigned_vects = [vectors[i] for i in range(len(vectors))
                                  if sess.run(assignments[i]) == cluster_n]
                #計算新的集羣中心點
                new_location = sess.run(mean_op, feed_dict={
                    mean_input: array(assigned_vects)})
                #爲每一個向量分配合適的中心點
                sess.run(cent_assigns[cluster_n], feed_dict={
                    centroid_value: new_location})
 
        #返回中心節點和分組
        centroids = sess.run(centroids)
        assignments = sess.run(assignments)
        return centroids, assignments

須要注意的是，若是

for i in range(100):
    x = sess.run(tf.assign(variable1, placeholder))

像上面那樣看似無害地在每次執行的時候建立一個新的OP（譬如tf.assign或者tf.zeros這樣的），這樣會必定的影響性能。做爲替代的，你應該爲每一個任務定義一個特定的OP，而後在循環中調用這個OP。能夠使用len(graph.get_operations())這個方法來檢測是否有冗餘的非必需的OPs。準確來講，sess.run應該是在迭代中惟一會與graph產生交互的方法。在上述代碼的138~139行中能夠看出，一系列的ops/Variables能夠組合在sess.run中使用。