程序猿修仙之路--算法之快速排序到底有多快

<img src="https://www.cnblogs.com/image...; width="100%" hegiht="20%" align=center />

分治思想

關於排序，江湖盛傳有一種分治思想,能大幅度提升排序心法的性能。所謂分治，即：化大爲小，分而治之。達到治小而治大的成效。多年來基於分治思想衍生出多種排序心法，然萬變不離其宗！

雖然江湖上算法內功繁多，可是好的算法小編認爲必須符合如下幾個條件，方能真正提升習練者實力。

• 時間複雜度（運行時間）

在算法時間複雜度維度，咱們主要對比較和交換的次數作對比，其餘不交換元素的算法，主要會以訪問數組的次數的維度作對比。

其實有不少修煉者對於算法的時間複雜度有點模糊，分不清什麼所謂的 O(n),O(nlogn),O(logn)...等，也許下圖對一些人有一些更直觀的認識。

• 空間複雜度（額外的內存使用）

排序算法的額外內存開銷和運行時間同等重要。 就算一個算法時間複雜度比較優秀，空間複雜度很是差，使用的額外內存很是大，菜菜認爲它也算不上一個優秀的算法。

• 結果的正確性

這個指標是菜菜本身加上的，我始終認爲一個優秀的算法最終獲得的結果必須是正確的。就算一個算法擁有很是優秀的時間和空間複雜度，可是結果不正確，致使修煉者經脈逆轉，走火入魔，又有什麼意義呢？

原理

基本思想：選取一個元素做爲分割點，經過遍歷把小於分割點的元素放到分割點左邊，把大於分割點的元素放到分割點元素右邊。而後再按此方法對兩部分數據分別排序，以此類推，直到分割的數組大小爲1。 整個排序過程能夠遞歸進行，以此達到整個數據變成有序序列。

過程

實現快速排序的方式有不少，其中以相似指針移動方式最爲常見，爲何最多見呢？由於它的空間複雜度爲O（1），也就是說是原地排序。

1. 咱們從待排序的記錄序列中選取一個記錄(一般第一個)做爲基準元素(稱爲key)key=arr[left]，而後設置兩個變量，left指向數列的最左部，right指向數據的最右部。

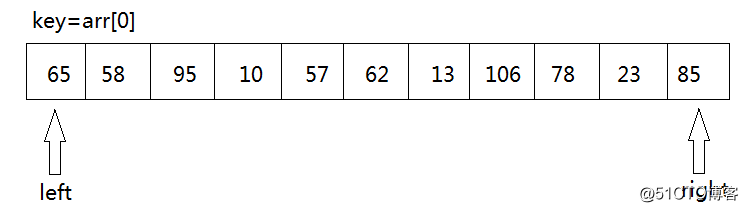
1. key首先與arr[right]進行比較，若是arr[right]<key，則arr[left]=arr[right]將這個比key小的數放到左邊去，若是arr[right]>key則咱們只須要將right--，right--以後，再拿arr[right]與key進行比較，直到arr[right]<key交換元素爲止。

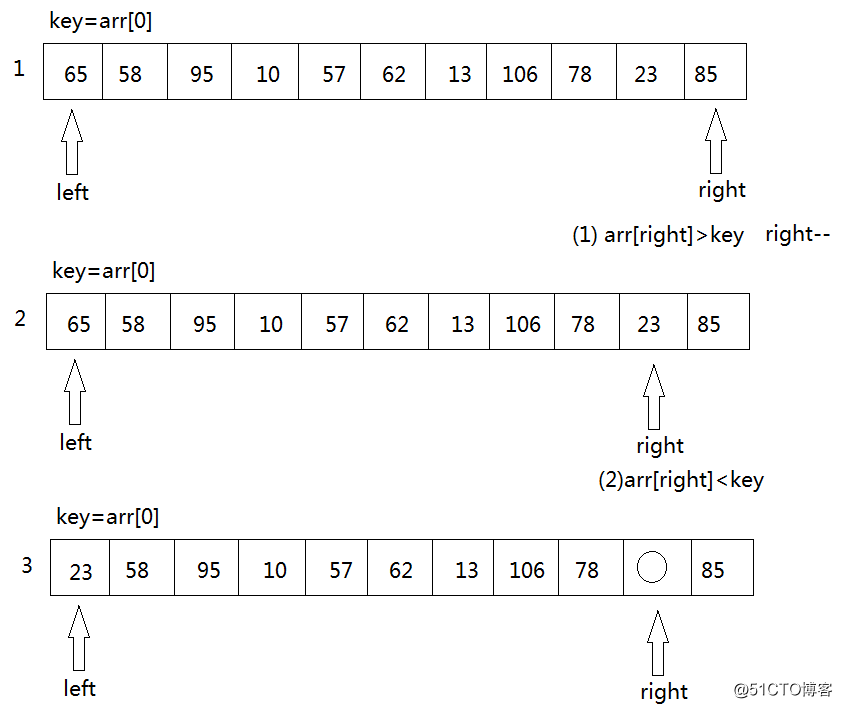
1. 若是右邊存在arr[right]<key的狀況，將arr[left]=arr[right]，接下來，將轉向left端，拿arr[left ]與key進行比較，若是arr[left]>key,則將arr[right]=arr[left]，若是arr[left]<key，則只須要將left++,而後再進行arr[left]與key的比較。

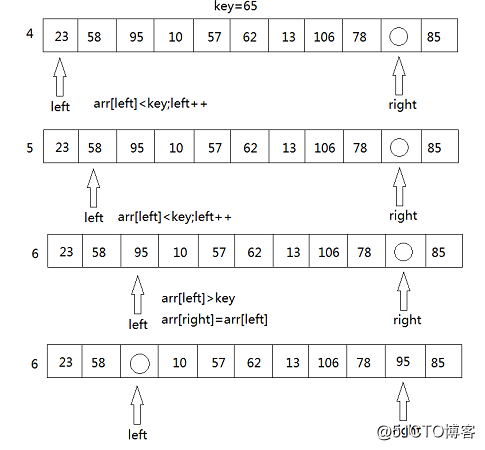
1. 而後再移動right重複上述步驟

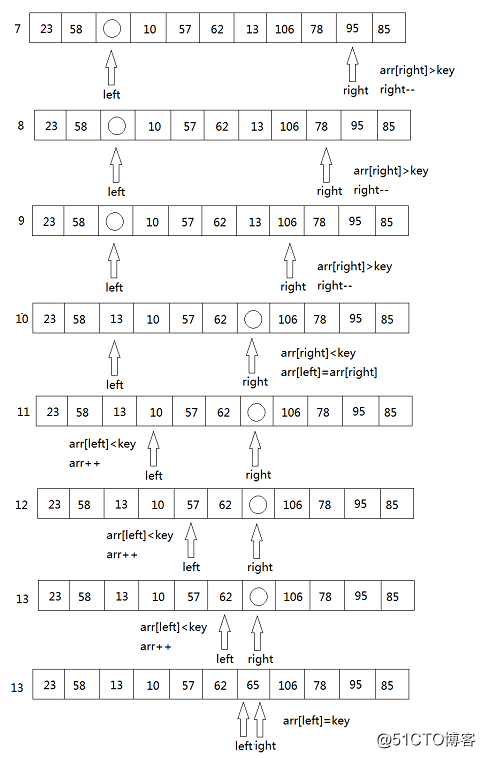
1. 最後獲得 {23 58 13 10 57 62} 65 {106 78 95 85}，再對左子數列與右子數列進行一樣的操做。最終獲得一個有序的數列。

{23 58 13 10 57 62} 65 {106 78   95 85}
{10 13} 23 {58 57 62} 65 {85 78 95} 106
10 13 23 57 58 62 65 78 85 95 106

性能特色

關於複雜度相關O（n）等公式，我這裏須要強調一點,公式表明的是算法的複雜度增加的趨勢，而不是具體計算複雜度的公式。好比：O（n²）和O（n）相比較，只是說明 O(n²)增加的趨勢要比o(n)快，並非說明O(n²)的算法比O(n)的算法所用時間必定就要多。

時間複雜度

快速排序平均時間複雜度爲O(nlogn),最好狀況下爲O(nlogn)，最壞狀況下O(n²)

空間複雜度

基於以上例子來實現的快排，空間複雜度爲O(1),也就是原地排序。

穩定性

舉個例子：
待排序數組:int a[] ={1, 2, 2, 3, 4, 5, 6};

在快速排序的隨機選擇比較子(即pivot)階段：
若選擇a[2]（即數組中的第二個2）爲比較子，，而把大於等於比較子的數均放置在大數數組中，則a[1]（即數組中的第一個2）會到pivot的右邊， 那麼數組中的兩個2非原序（這就是「不穩定」）。
若選擇a[1]爲比較子，而把小於等於比較子的數均放置在小數數組中，則數組中的兩個2順序也非原序。可見快速排序不是穩定的排序。

改進

經過以上分析各位俠士是否可以分析出來快速排序有哪些地方存在瑕疵呢？

1. 切分不平衡：也就是說咱們選取的切分元素距離數組中間值的元素位置很遠，極端狀況下會是數組最大或最小的元素，這就致使了劃分出來的大數組會被劃分爲不少次。針對此狀況，咱們能夠取數組多個元素來平衡這種狀況，例如：咱們能夠隨機選取三個或者五個元素，取其中間值的元素做爲分割元素。
2. 小數組：當快速排序切分爲比較小的數組時候，也會利用遞歸調用本身。在這種小數組的狀況下，其實一些基礎排序算法反而比快速排序要快。當數組比較小的時候不妨嘗試一下切換到插入排序。具體多小是小呢？通常5-15吧，僅供參考。
3. 重複元素：在咱們實際應用中常常會遇到重複元素比較多的狀況，按照快排的思想，相同元素是會被頻繁移動和劃分的，其實這徹底沒有必要。咱們該怎麼辦呢？咱們能夠把數組切換爲三部分：大於-等於-小於 三部分數組，這樣等於的那部分數組就能夠避免移動了，不過落地的代碼複雜度要高不少，有興趣的同窗能夠實現一下。

使用場景

1. 當一個數組大小爲中型以上的數量級時，菜菜認爲可使用快速排序，而且伴隨着數組的持續增大，快速排序的性能趨於平均運行時間。至於多大的數組爲中型，通常認爲50+ 吧，僅供參考。
2. 當一個數組爲無序而且重複元素很少時候，也適合快速排序。爲何提出重複元素這個點呢？由於若是重複元素過多，原本重複元素是無需排序的，可是快速排序仍是要劃分爲更多的子數組來比較，這個時候也許插入排序更適合。

試煉一發吧

c# 武器版

static void Main(string[] args)
        {
            List<int> data = new List<int>();
            for (int i = 0; i < 11; i++)
            {

                data.Add(new Random(Guid.NewGuid().GetHashCode()).Next(1, 100));
            }
            //打印原始數組值
            Console.WriteLine($"原始數據： {string.Join(",", data)}");
            quickSort(data, 0, data.Count - 1);
            //打印排序後的數組
            Console.WriteLine($"排序數據： {string.Join(",", data)}");
            Console.Read();
        }
        public static void quickSort(List <int> source, int left, int right)
        {
            int pivot = 0;
            if (left < right)
            {
                pivot = partition(source, left, right);
                quickSort(source, left, pivot - 1);
                quickSort(source, pivot + 1, right);
            }
        }
        //對一個數組/列表按照第一個元素 分組排序，返回排序以後key所在的位置索引
        private static int partition(List<int> source, int left, int right)
        {
            int key = source[left];
            while (left < right)
            {
                //從右邊篩選 大於選取的值的不動，小於key的交換位置
                while (left < right && source[right] >= key)
                {
                    right--;
                }
                source[left] = source[right];
                while (left < right && source[left] <= key)
                {
                    left++;
                }
                source[right] = source[left];
            }
            source[left] = key;
            return left;
        }

golang 武器版

package main

import (
    "fmt"
    "math/rand"
)

func main() {
    var data []int
    for i := 0; i < 10; i++ {
        data = append(data, rand.Intn(100))
    }
    fmt.Println(data)
    quickSort(data[:], 0, len(data)-1)
    fmt.Println(data)
}
func quickSort(source []int, left int, right int) {
    var pivot = 0
    if left < right {
        pivot = partition(source, left, right)                                        
        quickSort(source, left, pivot-1)
        quickSort(source, pivot+1, right)
    }
}

func partition(source []int, left int, right int) int {
    var key = source[left]
    for left < right {
        for left < right && source[right] >= key {
            right--
        }
        source[left] = source[right]
        for left < right && source[left] <= key {
            left++
        }
        source[right] = source[left]
    }
    source[left] = key
    return left
}

運行結果：

[81 87 47 59 81 18 25 40 56 0]
[0 18 25 40 47 56 59 81 81 87]

---

添加關注，查看更精美版本，收穫更多精彩