【機器學習】線性迴歸原理介紹

• 【機器學習】線性迴歸原理介紹
• 【機器學習】線性迴歸python實現
• 【機器學習】線性迴歸sklearn實現

一般咱們學習機器學習都是從線性迴歸模型開始的。線性迴歸模型形式簡單、易於建模，可是咱們能夠從中學習到機器學習的一些重要的基本思想。

迴歸一詞的由來：

這個術語是英國生物學家兼統計學家高爾頓在1886年左右提出來的。人們大概都注意到，子代的身高與其父母的身高有關。高爾頓以父母的平均身高X做爲自變量，其一成年兒子的身高Y爲因變量。他觀察了1074對父母及其一成年兒子的身高，將所得(X, Y)值標在直角座標系上，發現兩者的關係近乎一條直線，總的趨勢是X增長時Y傾向於增長，這是意料中的結果.有意思的是,高爾頓對所得數據作了深刻一層的考察，而發現了某種有趣的現象。

高爾頓算出這1074個X值的算術平均爲68英寸(1英寸爲2.54釐米)，而1074個Y值的算術平均爲69英寸，子代身高平均增長了1英寸，這個趨勢現今人們也已注意到。以此爲據，人們可能會這樣推想：若是父母平均身高爲a英寸，則這些父母的子代平均身高應爲a+1英寸，即比父代多1英寸。但高爾頓觀察的結果與此不符，他發現：當父母平均身高爲72英寸時，他們的子代身高平均只有71英寸,不只達不到預計的72+1=73英寸，反而比父母平均身高小了。反之,若父母平均身高爲64英寸，則觀察數據顯示子代平均身高爲67英寸，比預計的64+1=65英寸要多。

高爾頓對此的解釋是：大天然有一種約束機制，令人類身高分佈保持某種穩定形態而不做兩極分化。這就是種使身高「迴歸於中心「的做用。例如，父母身高平均爲72英寸，比他們這一代平均身高68英寸高出許多，「迴歸於中心」的力量把他們子代的身高拉回來些：其平均身高只有71英寸，反比父母平均身高小，但仍超過子代全體平均69英寸。反之，當父母平均身高只有64英寸，遠低於他們這代的平均值68英寸時，「迴歸於中心」的力量將其子代身高拉回去一些，其平均值達到67英寸，增加了3英寸，但仍低於子代全體平均值69英寸。

正是經過這個例子，高爾頓引人了「迴歸」這個名詞。

線性迴歸的模型形如：

線性迴歸得出的模型不必定是一條直線，在只有一個變量的時候，模型是平面中的一條直線；有兩個變量的時候，模型是空間中的一個平面；有更多變量時，模型將是更高維的。

線性迴歸模型有很好的可解釋性，能夠從權重W直接看出每一個特徵對結果的影響程度。

線性迴歸適用於X和y之間存在線性關係的數據集，可使用計算機輔助畫出散點圖來觀察是否存在線性關係。例如咱們假設房屋價格和房屋面積之間存在某種線性關係，畫出散點圖以下圖所示。

看起來這些點分佈在一條直線附近，咱們嘗試使用一條直線來擬合數據，使全部點到直線的距離之和最小。實際上，線性迴歸中一般使用殘差平方和，即點到直線的平行於y軸的距離而不用垂線距離，殘差平方和除以樣本量n就是均方偏差。均方偏差做爲線性迴歸模型的代價函數(cost function)。使全部點到直線的距離之和最小，就是使均方偏差最小化，這個方法叫作最小二乘法。

代價函數：

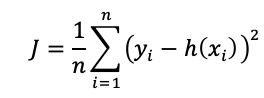
其中，

下面求使J最小的W和b：

1.偏導數法

偏導數法是很是麻煩的，須要一個一個地計算w。爲了方便，這裏以單變量線性迴歸爲例。

2.正規方程法

正規方程使用矩陣運算，能夠一次求出W向量。可是當變量(feature)個數大於數據個數時，會致使xTx不可逆，這時候就不能用此方法了。

使用正規方程法，若是但願獲得的模型帶有偏置項b，就要先給數據集X增長全爲1的一列，這樣纔會把b包含在W中；若是不添加，那麼模型是強制過原點的。

3.梯度降低

這裏的代價函數J的海森矩陣H是半正定的，所以J必定有全局最小值，因此也可使用梯度降低法來求解。梯度降低法是一種迭代解法，不只能夠求解最小二乘問題，也適用於其它代價函數的問題。可是須要設置學習率α，α設置的過大或太小，都不能很好地訓練出模型，並且梯度降低法須要對數據集進行特徵縮放。通常會在數據集特別大的時候或者xTx不可逆的時候使用梯度降低法，後面再作介紹。

4.其餘

還有一些方法就不一一列舉了。例如奇異值分解，QR分解，喬姆斯基分解等等。

計算出的模型以下圖。

再放一個兩個變量的狀況的，以下圖。