「袁創」正交設計，OO 與 SOLID

正交設計，是廣泛的設計原則，與粒度無關，與編程範式無關，更與具體的實現語言無關。（雖然確實在不一樣的編程範式下，或使用不一樣的編程語言時，具體的解決方法或難易程度不一樣，這也正是爲什麼咱們老是在尋找更適合的編程範式，更高效的編程語言的緣由）。

而具體到面向對象範式，咱們都知道著名的SOLID原則。可是：這五個原則是怎麼來的？它們的目的和在？它們的關係如何？

爲了搞清楚這些疑問，咱們再次回到最初的問題：

1. 軟件模塊該如何劃分？（怎麼分）

2. 模塊間API該如何定義？（怎麼合）

怎樣進行分解？

模塊的劃分，是一個問題分解的過程。

在文章《VBD (Volatility Based Decomposition)》裏，引用了一篇70年代的論文《On the Criteria to be Used in Decomposing Systems into Modules》。

在這篇論文裏，做者經過一個小例子，清晰的指出了軟件模塊劃分應該以基於信息隱藏爲目的，以職責劃分爲手段，從而封裝變化，讓軟件更加容易修改（即Kent Beck的理想：局部化影響）。

這篇文章也展現了：基於流程（過程）的分解，是一種極其脆弱的模塊劃分方式。於是咱們應該離基於過程的分解越遠越好。

這也是爲什麼Matt Cochran將這種分解方法稱作：基於易變性的分解（Volatility Based Decomposition）。

總而言之，變化及應對變化，是軟件設計最大的挑戰，目的和意義。

面向對象究竟要解決什麼問題？

最近幾年，我聽到太多針對OO的批評，其中最爲奇葩的說法是：OO只適合GUI編程。由於GUI組件概念上更接近於對象，至於其它領域則不太合適。

對提出這樣高論的人，我至關確信，他們不只對於面向對象一無所知，更是對於複雜軟件所面臨的真正挑戰，以及軟件設計究竟要解決什麼問題一無所知。

前兩天偶然從東海陳光劍的文章《函數式編程與面向對象編程[5]:編程的本質》讀到軟件模塊化的目的和價值（雖然他用的是結構化，但在我看來也是在談模塊化），很是精彩，深合我意：

（軟件設計是一個）層次化分解與從新複合的過程

這個思惟過程, 並不是是受計算機的限制而產生，它反映的是人類思惟的侷限性。咱們的大腦一次只能處理不多的概念。生物學中被廣爲引用的 一篇論文指出咱們咱們的大腦中只能保存7 ± 2個信息塊。咱們對人類短時間記憶的認識可能會有變化，可是能夠確定的是它是有限的。底線就是咱們不能處理一大堆亂糟糟的對象或像蘭州拉麪似的代碼。

咱們須要結構化並不是是由於結構化的程序看上去有多麼美好，而是咱們的大腦沒法有效的處理非結構化的東西。咱們常常說一些代碼片斷是優雅的或美觀的，實際上那隻意味 着它們更容易被人類有限的思惟所處理。優雅的代碼創造出尺度合理的代碼塊，它正好與咱們的『心智消化系統』可以吸取的數量相符。

那麼，對於程序的複合而言，正確的代碼塊是怎樣的？它們的表面積必需要比它們的體積增加的更爲緩慢。我喜歡這個比喻，由於幾何對象的表面積是以尺寸的平方的速度增加的，而體積是以尺寸的立方的速度增加的，所以表面積的增加速度小於體積。

代碼塊的表面積是是咱們複合代碼塊時所須要的信息。代碼塊的體積 是咱們爲了實現它們所須要的信息。一旦代碼塊的實現過程結束，咱們就能夠忘掉它的實現細節，只關心它與其餘代碼塊的相互影響。在面向對象編程中，類或接口的聲明就是表面。在函數式編程中，函數的聲明就是表面。我把事情簡化了一些，可是要點就是這些。

怎樣才能作到表面積增加速度小於體積增加速度？固然是分解，信息隱藏，抽象。而這些也正是面向對象所追求和擅長的。

面向對象主要目的是爲了模塊化。雖然在一些數學家看來：因爲面向對象沒有很好的數學理論基礎，於是必然是一個錯誤的方法論。可對於如何編寫一個易於應對變化的軟件，並非一個純數學理論問題（或許確實有數學家也能夠抽象出一套數學理論），而更多的是一個實踐問題。做爲長期處於實踐一線的咱們，不該把幾個數學家的見解看成金科玉律（對於那些沒有實踐經驗，卻對如何實踐指手畫腳的純理論派，每次看到他們的不負責任的言論，考慮到他們的影響力和對新手的誤導，就禁不住想對他們豎中指）（參見《學習的邏輯3: 三人行必有我徒》）。

軟件工業最近20年來，可以構建如此大規模的需求頻繁變化的軟件系統，很大程度上得益於面向對象對於模塊化的良好支持。

而如今風頭正勁的微服務化，無非是把模塊化的思想，從進程內模塊（類），變爲進程間而已。

OO和FP

面向對象與函數式編程的最大區別在於數據是不是強制不變性。這個前提，致使了一系列其它的差別。

由於可變性，面向對象能夠將算法和數據放在一塊兒，當數據是一種實現細節時，可對其進行信息隱藏和封裝。但在Pure FP裏，數據和算法是必須分離的。這種分離，在不少場景下，對於信息隱藏至關不利（在這裏咱們先不談性能）。於是，當系統規模足夠複雜時，FP對於構造易於維護軟件的能力比面向對象要弱。

於是，FP爲了實用，要麼部分放棄對不變性的堅持（如LISP所作的那樣），從而容許模擬面向對象範式（參見SICP）；要麼經過Existential Quantification，來模擬OO的運行時多態，以達到信息隱藏，隔離變化的目的；要麼使用輕量級進程（輕量很關鍵）：讓每一個輕量級進程承擔一個很小的職責，從進程外部看，每一個輕量級進程均可以有可修改的數據，以及基於消息的行爲驅動（如erlang或akka的Actor模型），而這正是對於smalltalk的對象模擬，從而緩解了不變性帶來的尷尬。進而也說明了基於高內聚，低耦合原則進行的模塊化是超越範式的。

於是，一些FPer對於OO的盲目批評，和認爲面向對象只適合GUI領域同樣，都並不真正明白一個複雜軟件的關鍵挑戰，以及解決方案何在。

固然，具體到編程語言，即使都是OO語言，差異也巨大。但這是另一個宏大的話題，這裏暫且不談。只重點說一句：不要把某種OO語言，看成OO自己。

關於FP和OO的話題，值得專門寫一篇文章全面論述，而本文的目的在於介紹SOLID，於是再也不贅述。

正交原則與SOLID的關係

一個好的面向對象設計，天然是符合高內聚，低耦合原則的對象劃分和協做方式。

單一職責和開放封閉，更多的在強調類劃分時的高內聚；而里氏替換，依賴倒置，接口隔離則更多的強調類與類之間協做接口（即API）定義的低耦合。

高內聚（怎麼分）

單一職責，經過對變化緣由的識別，將一個承擔多重職責的類，不斷分割爲更小的，只具有單一變化緣由的類。而單一變化緣由指的是：一個變化，會引發整個類都發生變化。只有關聯極其緊密的狀況，纔會致使這樣的局面。於是，單一職責和高內聚某種程度是同義詞。

但單一職責原則自己，並無明確指示咱們該如何斷定一個類屬於單一職責的，以及如何達到單一職責的狀態。而策略消除重複，分離不一樣變化方向，正是讓類達到單一職責的策略與途徑。

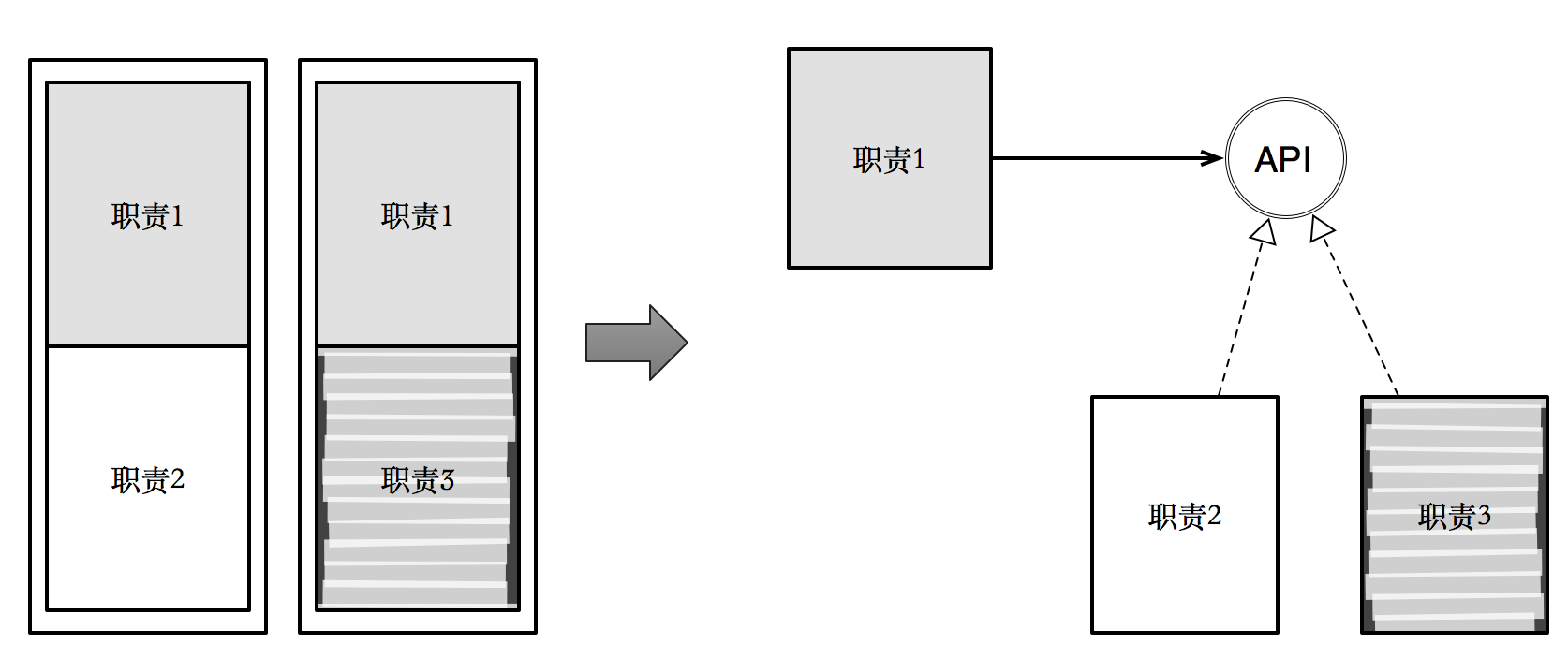
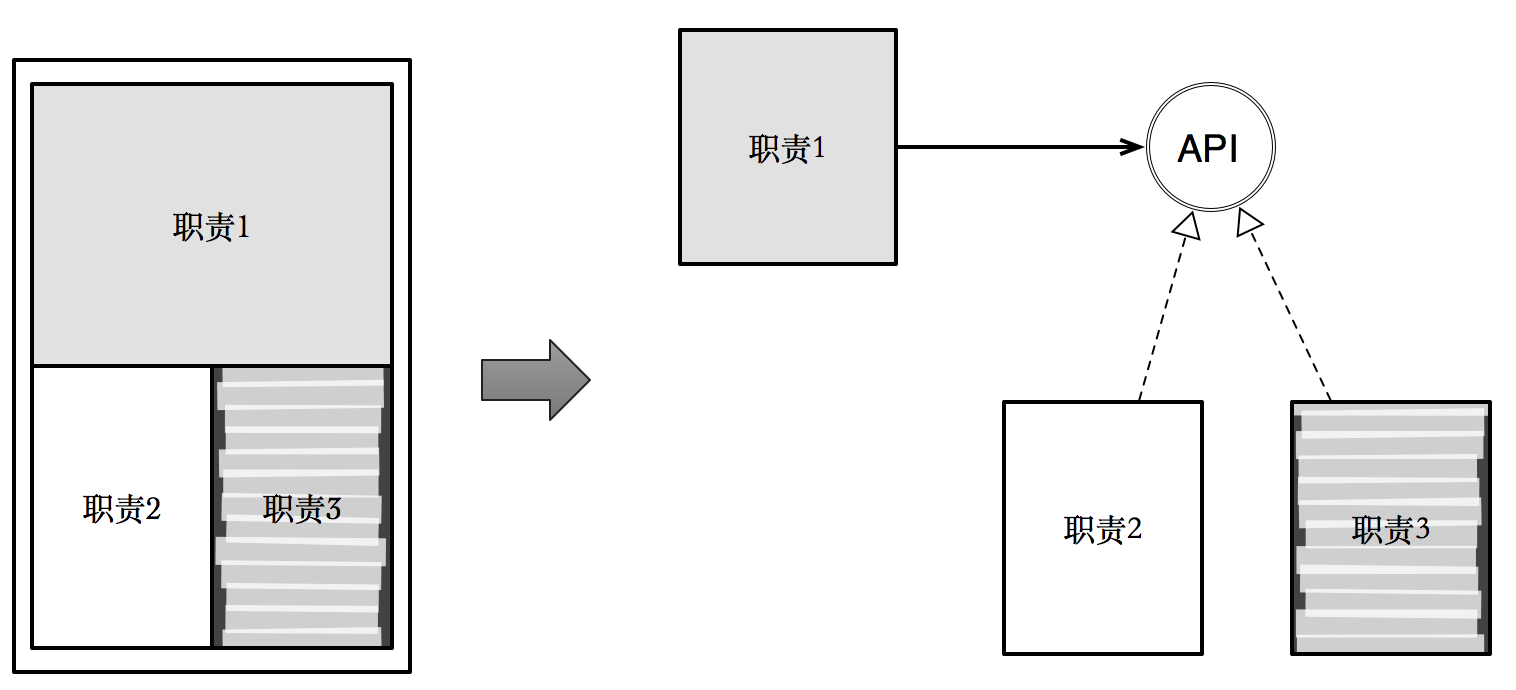
低耦合 (怎麼合)

而開放封閉原則，正是經過將不一樣變化方向進行分離，從而達到對於已經出現的變化方向，對於修改是封閉的，對於擴展是開放的。

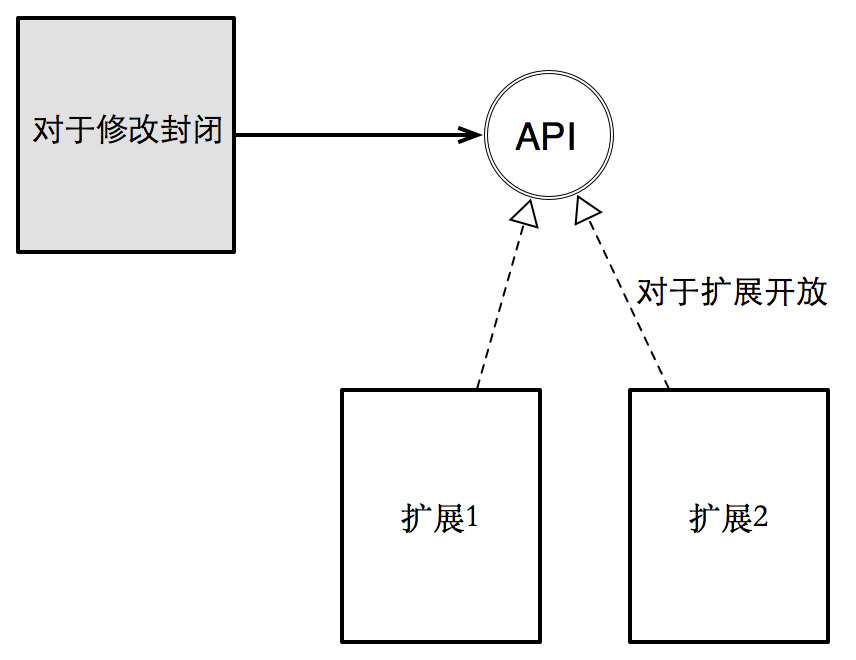
里氏替換原則強調的是，一個子類不該該破壞其父類與客戶之間的契約。惟有如此，才能保證：客戶與其父類所暴露的接口（即API）所產生的依賴關係是穩定的。子類只應該成爲隱藏在API背後的某種具體實現方式。

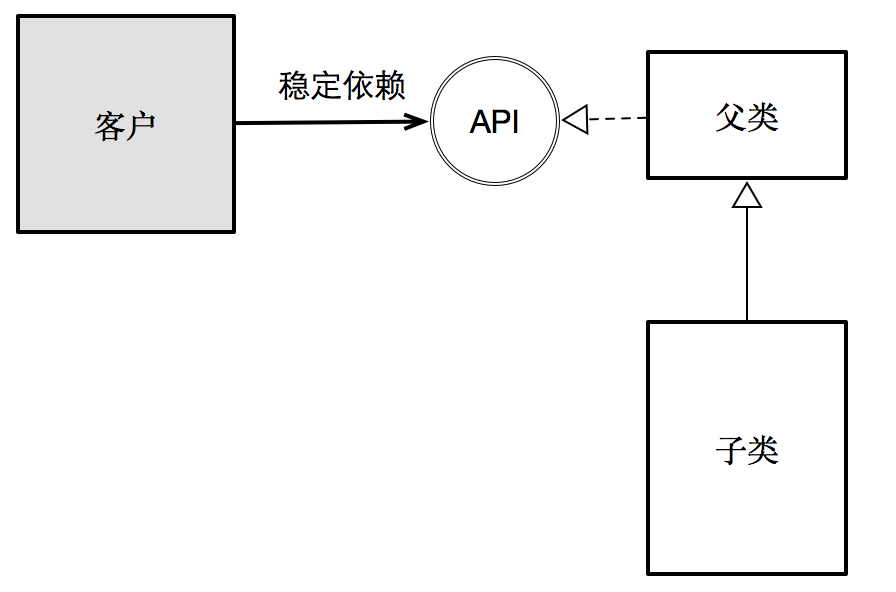
依賴倒置原則則強調：爲了讓依賴關係是穩定的，不該該由實現側根據本身的技術實現方式定義接口，而後強迫上層（即客戶）依賴這種不穩定的API定義，而是應該站在上層（即客戶）的角度去定義API（正所謂依賴倒置）。

可是，雖然接口由上層定義，但最終接口的實現卻依然由下層完成，所以依賴倒置描述爲：上層不依賴下層，下層也不依賴上層，雙方共同依賴於抽象。

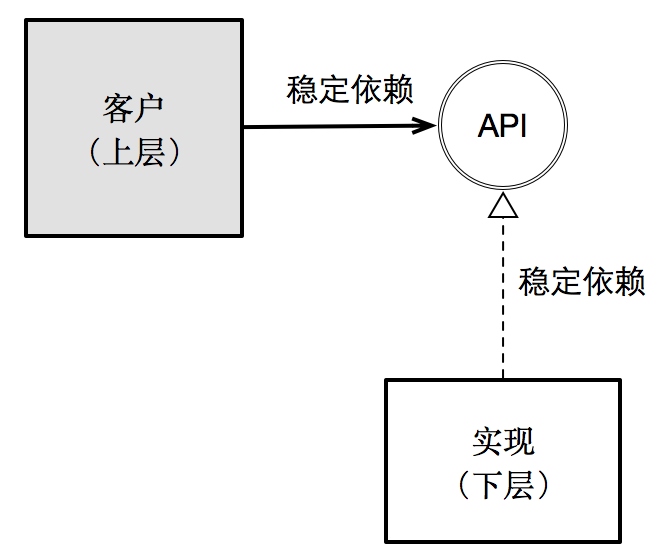
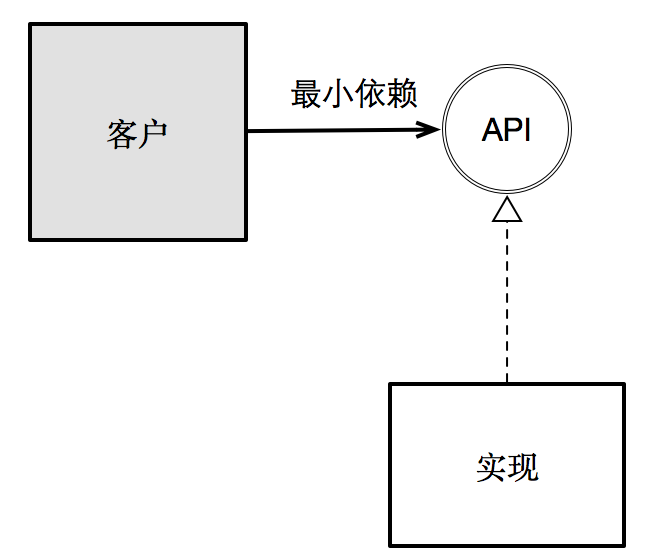
最後，接口隔離原則強調的是：不該該強迫客戶依賴它不須要的東西。顯然，這是縮小依賴範圍策略在面向對象範式下的產物。

結論

正交設計是一種與範式，語言無關的設計原則。爲了解決在模塊化的過程當中，如何讓軟件在長期範圍內更容易應對變化。

而面向對象是一種對模塊化支持良好的範式。經過高內聚，低耦合原則，或正交策略的運用，面向對象範式下SOLID原則會天然浮現。

咱們耳熟能詳的軟件設計相關原則，模式與實踐的關係以下：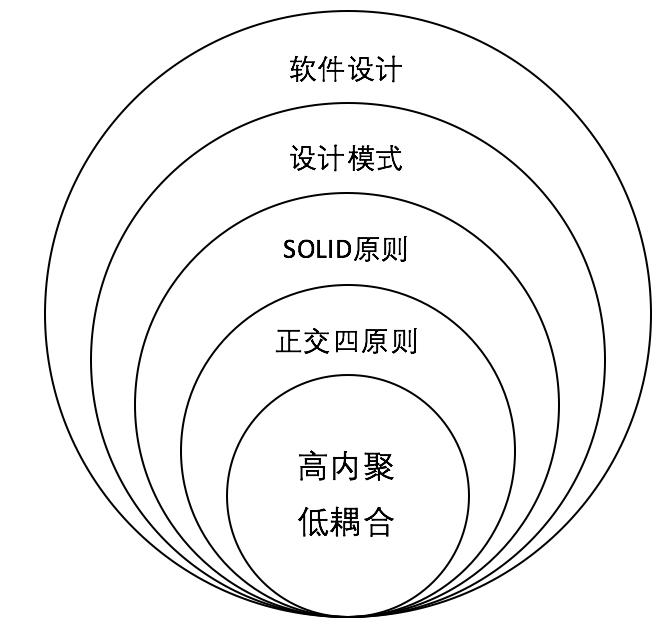

關於正交設計的更多細節，請參閱《變化驅動：正交設計》。