瘋狂kotlin講義連載之運算符和表達式——位運算符

時間 2019-12-04

標籤瘋狂 kotlin 講義連載運算符表達式简体版

原文原文鏈接

3.2 位運算符

Kotlin 雖然也提供了與 Java 功能徹底相同的位運算符，但這些位運算符都不是以特殊字符給出的，而是以infix函數的形式給出的，所以程序只能用函數名來執行這些位運算符。

Kotlin 支持的位運算符一樣有以下 7 個。

一、 and(bits) ：按位與。當兩位同時爲 1 時才返回 1 。

二、 or(bits) ：按位或。只要有一位爲 1 便可返回 1 。

三、 inv(bits)：按位非。單目運算符，將操做數的每一個位（包括符號位）所有取反。

四、xor(bits)：按位異或。當兩位相同時返回0，不一樣時返回1。算法

五、 shl(bits：左移運算符。

六、shr(bits)：右移運算符。函數

七、 ushr(bits)：無符號右移運算符。

Kotlin 位運算符的只能對 Int 或 Long 兩種數據類型起做用。位運算符的運算法則如表 3.10 所示。

3.10表

位運算符的運算法則

第一個運算數	第二個運算數	按位與	按位或	按位異或
0	0	0	0	0
0	1	0	1	1
1	0	0	1	1
1	1	1	1	0

按位非只須要一個操做數，這個運算符將把操做數在計算機底層的二進制碼按位（包括符號位）取反。以下代碼測試了按位與和按位或運算的運行結果。

程序清單：

codes\03\3.2\BitOperatorTest.kt
println(5 and 9) // 將輸出 1

println(5 or 9) // 將輸出 13

程序執行的結果是：

5 and 9 的結果是 1 ， 5 or 9 的結果是 13 。下面介紹運算原理。

5 的二進制碼是 00000101 （省略了前面的 24 個 0 ），而 9 的二進制碼是 00001001 （省略了前面的 24 個 0 ）。運算過程如圖 3.1 所示。

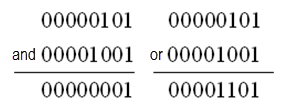
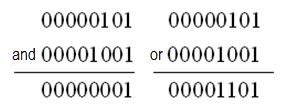
圖 3.1 按位與和按位或運算過程

下面是按位異或和按位取反的執行代碼（程序清單同上）。
println((-5).inv()) // 將輸出 4

println(5 xor 9) // 將輸出 12

程序執行 -5按位取反的結果是4，執行5 xor 9的結果是12，下面經過圖3.2 來介紹運算原理。

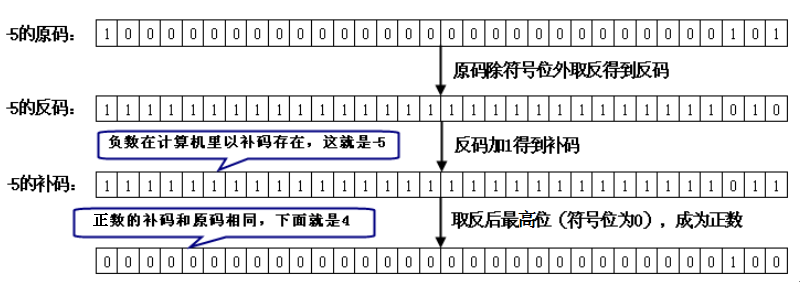
圖 3.2 -5 按位取反的運算過程

而 5 xor 9 的運算過程如圖 3.3 所示。

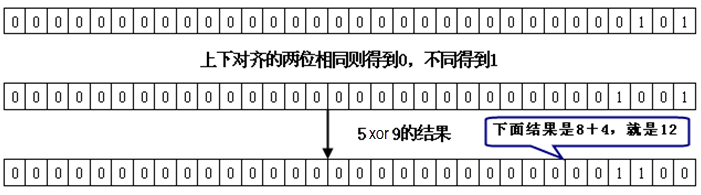
圖 3.3 5 xor 9 的運算過程

左移運算符是將運算數的二進制碼總體左移指定位數，左移後右邊空出來的位以 0 填充。例如以下代碼（程序清單同上）：

println(5 shl 2) // 輸出 20

println(-5 shl 2) // 輸出 -20

下面以-5爲例來介紹左移運算的運算過程，如圖3.4所示。

圖3.4 -5左移兩位的運算過程

在圖3.4中，上面的32位數是-5的補碼，左移兩位後獲得一個二進制補碼，這個二進制補碼的最高位是1，代表是一個負數，換算成十進制數就是-20。

Kotlin 的右移運算符有兩個：shr 和 ushr ，對於 shr

運算符而言，把第一個操做數的二進制碼右移指定位數後，左邊空出來的位以原來的符號位填充，即若是第一個操做數原來是正數，則左邊補 0 ；若是第一個操做數是負數，則左邊補 1 。

ushr 是無符號右移運算符，它把第一個操做數的二進制碼右移指定位數後，左邊空出來的位老是以 0 填充。

看下面代碼（程序清單同上）：

//輸出-2post

println(-5 shr 2)測試

//輸出1073741822spa

println(-5 ushr 2)3d

下面用示意圖來講明 shr 和 ushr 運算符的運算過程。

從圖3.5 來看， -5右移2位後左邊空出2位，空出來的2位以符號位補充。從圖中能夠看出，右移運算後獲得的結果的正負與第一個操做數的正負相同。右移後的結果依然是一個負數，這是一個二進制補碼，換算成十進制數就是-2。

圖3.5-5 右移2 位的運算過程

從圖3.6 來看，-5無符號右移2位後左邊空出2位，空出來的2位以0補充。從圖中能夠看出，無符號右移運算後的結果老是獲得一個正數。圖3.6 中下面的正數是1073741822（230-2）。

圖3.6-5 無符號右移2 位的運算過程

進行移位運算時還要遵循以下規則。

一、對於 Int 類型的整數移位 a shr b，當b>32時，系統先用b對32 求餘（由於 Int 類型只有 32位），獲得的結果纔是真正移位的位數。例如，a shr 33和a shr 1的結果徹底同樣，而a shr 32的結果和a相同。

二、對於 Long類型的整數移位a shr b，當b>64時，老是先用b對64求餘（由於Long類型是64位），獲得的結果纔是真正移位的位數。

注意：當進行移位運算時，只要被移位的二進制碼沒有發生有效位的數字丟失（對於正數而言，一般指被移出的位所有都是 0 ），不難發現左移 n 位就至關於乘以 2 的 n 次方，右移 n 位則是除以 2 的 n 次方。不只如此，進行移位運算不會改變操做數自己，只是獲得了一個新的運算結果，而原來的操做數自己是不會改變的。

以上內容節選自《瘋狂Kotlin講義》：一本讓您最直接認識Kotlin的瘋狂講義code