數據結構與算法——堆的應用

1. 概述

前面說完了堆這種數據結構，而且講到了它很經典的一個應用：堆排序，其實堆這種數據結構還有其餘不少的應用，今天就一塊兒來看看，主要有下列內容：

• 優先級隊列
• 求 Top K 問題
• 求中位數

2. 優先級隊列

優先級隊列是一種特殊的隊列，前面學習隊列的時候，說到隊列知足 先進先出，後進後出 的特色，優先級隊列則不是這樣。優先級隊列中的數據，出隊的順序是有優先級的，優先級高的，先出隊列。

而堆其實就能夠看做是一個優先級隊列，由於堆頂元素老是數據中最大或最小的元素，每次出隊列均可以看做取出堆頂元素。

若是你熟悉 Java 語言，則或多或少據說或是使用過 PriorityQueue 這個容器，在《Java 核心技術·卷 I》中，說到 PriorityQueue 就是優先級隊列，而且它基於一種很優雅的數據結構——堆。

接下來就小試牛刀，舉一個具體的例子來看看優先級隊列的應用。例如咱們須要合併 10 個有序的小文件，小文件中存儲的是有序的字符串數據。藉助優先級隊列，咱們能夠很高效的解決這個問題。

咱們從每一個文件中讀取第一個字符串存入優先級隊列中，那麼每次出隊列，都是最小的那個元素。將出隊列的數據存儲到一個大文件中，而後繼續從文件中讀取一個字符串存入隊列，而後繼續出隊列，一直循環這個操做。

固然，這主要是針對數據文件較大的狀況，若是數據很少，那麼直接將所有的數據存入隊列，而後依次出隊列就能夠了，具體問題具體分析。

3. Top K 問題

這樣的問題其實很是的常見了，在一組數據當中 ，咱們須要求得其前 K 大的數據。

這分爲了兩種狀況，一是針對 靜態數據 ，即數據不會發生變化。咱們能夠維護一個大小爲 K 的小頂堆，而後依次遍歷數組，若是數組數據比堆頂元素大，則插入到堆中，若是小，則不作處理。遍歷完以後，則堆中存在的數據就是 Top K 了。我用代碼模擬了這個過程：

public class GetTopK {
    public static void main(String[] args) {
        int[] num = {2, 34, 45, 56, 76, 65, 678, 33, 888, 678, 98, 0, 7};

        //求 Top 3
        Queue<Integer> queue = new PriorityQueue<>(3);
        queue.add(num[0]);
        queue.add(num[1]);
        queue.add(num[2]);

        for (int i = 3; i < num.length; i++) {
            int small = queue.peek();
            if (num[i] > small){
                queue.poll();
                queue.add(num[i]);
            }
        }
        System.out.println(queue.toString());
    }
}

第二種狀況，是動態的數據集合，數據會有增長、刪除的狀況，若是新增一個元素，將其和堆頂元素進行比較，若是數據比堆頂元素大，則插入到堆中，若是小，則不作處理。這樣的話，不管數據怎樣變化，咱們都可以隨時拿到 Top K，而不用由於數據的變化從新組織堆。

4. 求中位數

顧名思義，中位數就是一組數據中最中間的那個數據，只不過注意，數據須要有序排列。針對一個大小爲 n 的數據集，若是 n 爲偶數，那麼中位數有兩個，分別是 n/2 和 n/2 + 1 這兩個數據，咱們能夠隨機取其中一個；若是 n 爲奇數，則 n/2 + 1 這個數爲中位數。

若是是一個靜態的數據，那麼可直接排序而後求中位數，可是若是數據有變化，這樣每次排序的成本過高了。因此，能夠藉助堆來實現求中位數的功能。

咱們能夠維護一個大頂堆，一個小頂堆，小頂堆中存儲後 n/2 個數據，大頂堆中存儲前面剩餘的數據。若是 n 是偶數，則兩個堆中存儲的都是相同個數的數據，若是 n 爲奇數，則大頂堆中要多一個數據。結合下圖你就很容易明白了：

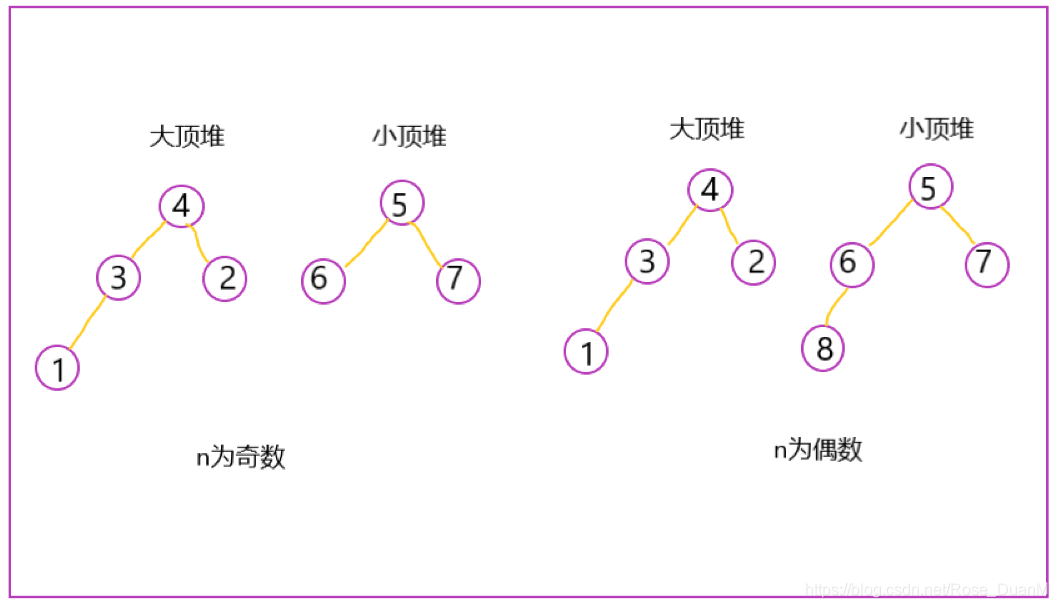
若是有數據插入的狀況，若是數據小於等於大頂堆頂元素，則插入到大頂堆中，若是數據大於等於小頂堆頂元素，則插入到小頂堆中。只不過可能會出現一個問題，就是堆中的數據不知足均分狀況，那麼咱們須要移動兩個堆中的元素，反正須要保證 大頂堆的元素個數和小頂堆的元素個數要麼相等，或者大頂堆中多一個。

我用代碼簡單模擬了整個實現：

public class GetMiddleNum {
        public static void main(String[] args) {
            //原始數據
            Integer[] num = {12, 34, 6, 43, 78, 65, 42, 33, 5, 8};
            //排序後存入ArrayList中
            Arrays.sort(num);
            ArrayList<Integer> data = new ArrayList<>(Arrays.asList(num));
            //大頂堆
            Queue<Integer> bigQueue = new PriorityQueue<>((o1, o2) -> {
                if (o1 <= o2) return 1;
                else return -1;
            });
            //小頂堆
            Queue<Integer> smallQueue = new PriorityQueue<>();
    
            int n = data.size();
            int i;
            if (n % 2 == 0) i = n / 2;
            else i = n / 2 + 1;
    
            //後 n/2 的數據存入到小頂堆中
            for (int j = i; j < n; j++) {
                smallQueue.add(data.get(j));
            }
            //前面的數據存入到大頂堆中
            for (int j = 0; j < i; j++) {
                bigQueue.add(data.get(j));
            }
    
            //插入數據，須要作單獨的處理
            insert(data, 99, bigQueue, smallQueue);
            insert(data, 3, bigQueue, smallQueue);
            insert(data, 1, bigQueue, smallQueue);
    
            //大頂堆的堆頂元素就是中位數
            System.out.println("The middle num = " + bigQueue.peek());
        }
    
        private static void insert(List<Integer> list, int value, Queue<Integer> bigQueue, Queue<Integer> smallQueue){
            list.add(value);
            if (value <= bigQueue.peek())
                bigQueue.add(value);
            if (value >= smallQueue.peek())
                smallQueue.add(value);
    
            while (smallQueue.size() > bigQueue.size())
                bigQueue.add(smallQueue.poll());
            while (bigQueue.size() - smallQueue.size() > 1)
                smallQueue.add(bigQueue.poll());
        }
    }