數據結構與算法——堆

1. 什麼是堆

堆（Heap），實際上是一種特殊的二叉樹，主要知足了二叉樹的兩個條件：

1. 堆是一種徹底二叉樹，還記得徹底二叉樹的定義嗎？葉節點都在最底下兩層，最後一層的節點都靠左排列，而且除了最後一層，其餘層的節點個數都要達到最大，這種樹叫作徹底二叉樹。
2. 堆中的每一個節點的值都必須大於等於（或者小於等於）其左右子節點的值。

對於堆中的每一個節點都大於等於其左右子節點的值，叫作大頂堆，反之，則叫作小頂堆。看看下面的圖就能懂了。

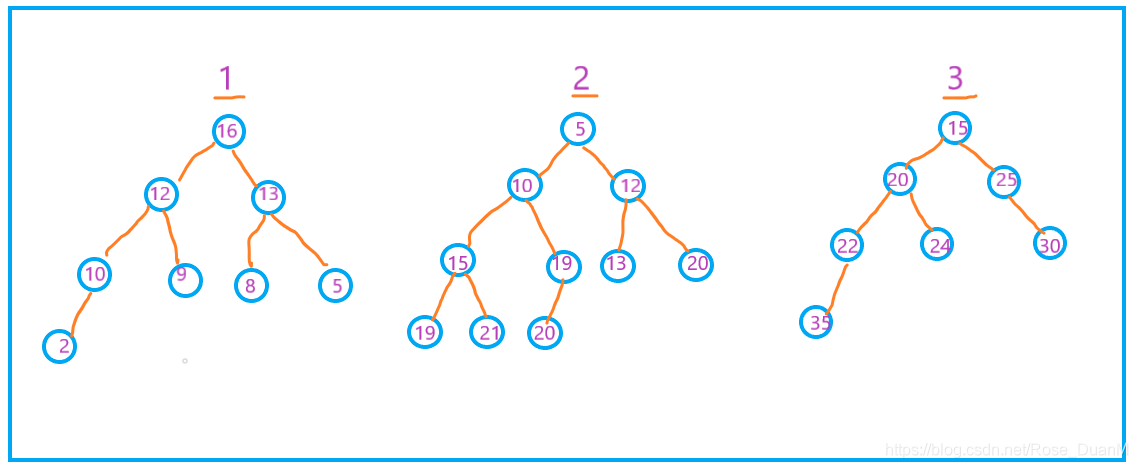
其中，1 是大頂堆，2 是小頂堆，3 不是堆。

2. 堆是如何存儲的？

其實，堆能夠按照徹底二叉樹的存儲方式來儲存，由於徹底二叉樹是比較省空間的，因此咱們能夠直接用數組來存儲，而後按照數組下標來取出堆中數據。參照下圖，來看看堆的存儲：

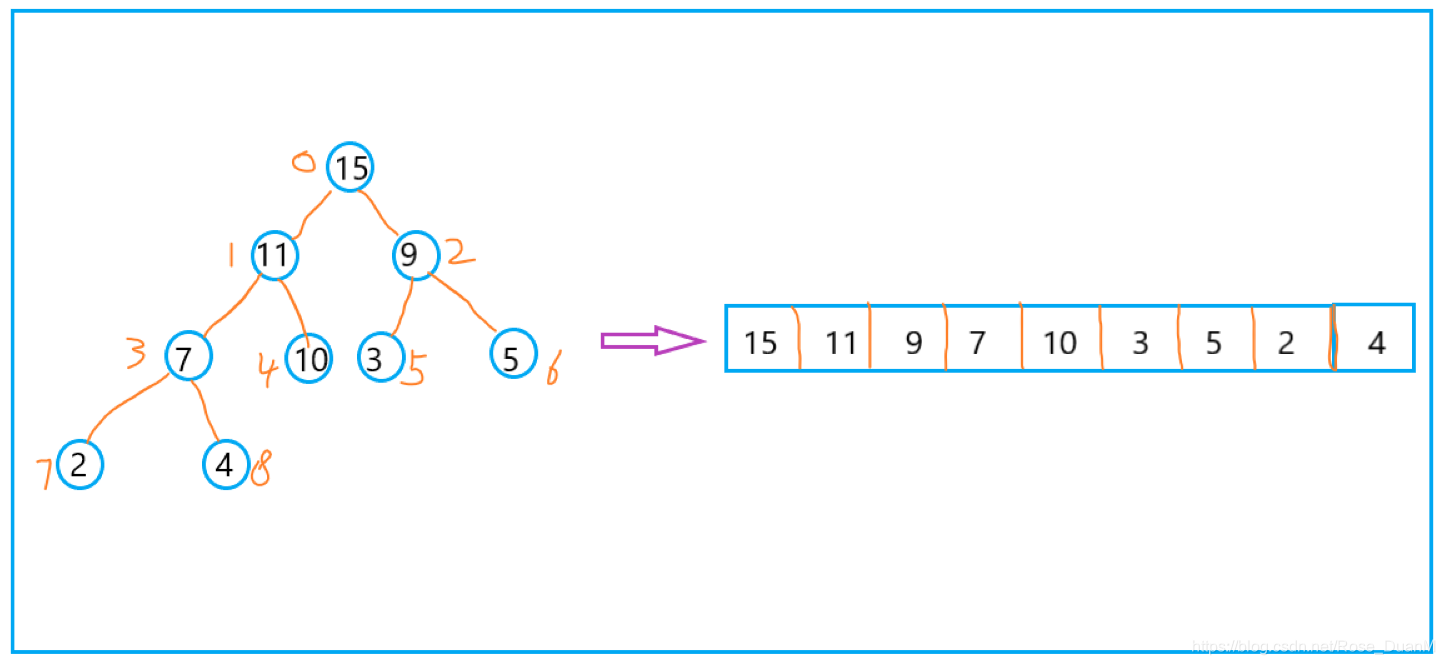
其中，對於任意位置上的節點 i ，其左子節點是 2 * i + 1，右子節點是 2 * i + 2，父節點是 (i - 1) / 2。

3. 堆的幾種操做

明白了堆是怎樣儲存的，咱們在來看看堆最多見的兩個操做：往堆中插入元素和刪除堆頂元素。

首先，若是要往堆中插入一個元素，咱們先將其插入到數組中最後一個位置，而後與其父節點的值進行比較，若是大於父節點，則交換位置，繼續比較。看看下面的圖你就明白了：

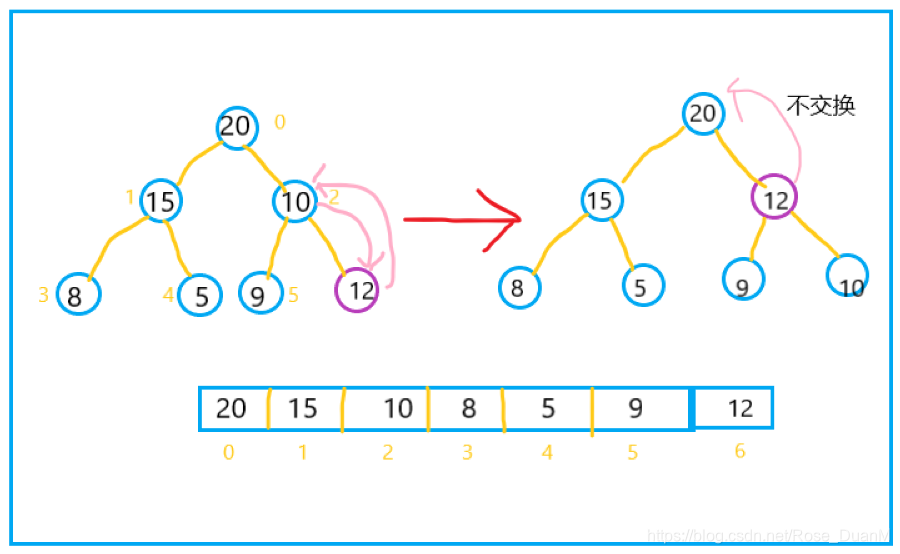
交換操做的代碼，我也放到這裏：

public class Heap {
    private int[] data;//存儲堆數據的數組
    private int n;//堆中可存儲的元素容量
    private int size;//堆中存儲的元素個數

    public Heap(int capacity) {
        this.data = new int[capacity];
        this.n = capacity;
        this.size = 0;
    }

    //往堆中插入數據
    public void insert(int value){
        if (size >= n) return;//堆滿了
        data[size] = value;
        int i = size;

        while ((i - 1) / 2 >= 0 && data[i] > data[(i - 1) / 2]){
            //交換data[i] 極其父節點 data[(i - 1) / 2] 的值
            swap(data, i, (i - 1) / 2);
            i = (i - 1) / 2;
        }
        size ++;
    }
    
    //交換數組兩個位置的元素
    private void swap(int[] data, int i, int j){
        int temp = data[i];
        data[i] = data[j];
        data[j] = temp;
    }
}

接下來看看第二種操做：刪除堆頂元素。

根據堆的定義，堆頂元素其實就是堆的最大或最小元素。因此刪除堆頂元素，咱們只須要移除數組中的第 0 個元素，而後再進行堆化，讓堆繼續保持順序。那該怎麼進行堆化呢？

首先咱們直接將堆中的最後一個元素移到堆頂，而後與其左右子節點的值進行比較，找到較大的那麼子節點，交換位置，而後繼續比較，你能夠結合代碼來理解一下：

//刪除數據，若是是大頂堆，則刪除的是堆中的最大元素
    //若是是小頂堆，則刪除的堆中的最小元素
    public int removeMax(){
        if (size == 0) return -1;//堆爲空
        //將數組中的最後一個元素，放到第一個位置
        int result = data[0];
        data[0] = data[size - 1];
        data[-- this.size] = 0;
        //進行堆化
        heapify(data, size, 0);
        return result;
    }
    
    //堆化函數
    private void heapify(int[] data, int size, int i){
        while (true){
            int max = i;
            if ((2 * i + 1) < size && data[i] < data[2 * i + 1]) max = 2 * i + 1;
            if ((2 * i + 2) < size && data[max] < data[2 * i + 2]) max = 2 * i + 2;
            if (max == i) break;
            swap(data, i, max);
            i = max;
        }
    }

4. 堆排序

如今來看看裏用堆這種數據結構是怎麼實現排序功能的。堆排序的時間複雜度很是的穩定，是O(nlogn)，而且是原地排序算法，具體是怎麼實現的呢？咱們通常把堆排序分爲兩個步驟：建堆和排序。

建堆
對於一個未排序的數組，例如 data[3,5,8,2,1,4,6]，其原始的結構是這樣的：

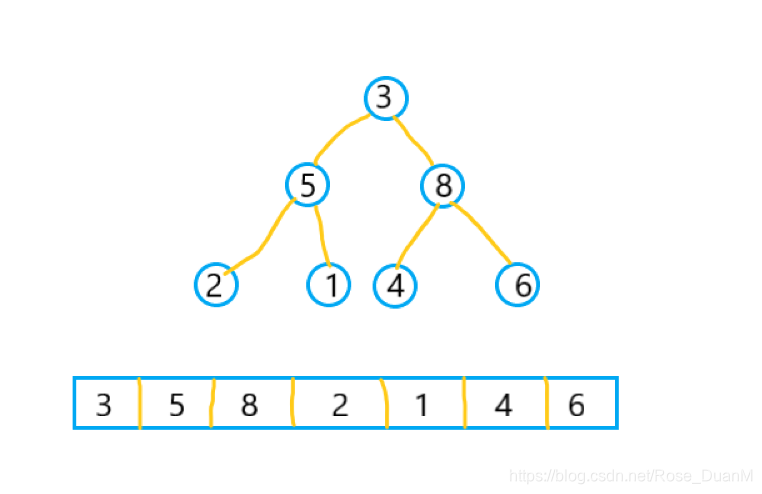
能夠看到第一個非葉子節點是 8，因此咱們從 8 開始從上往下堆化，而後依次是 5 - 3，堆化後的效果就是這樣的：

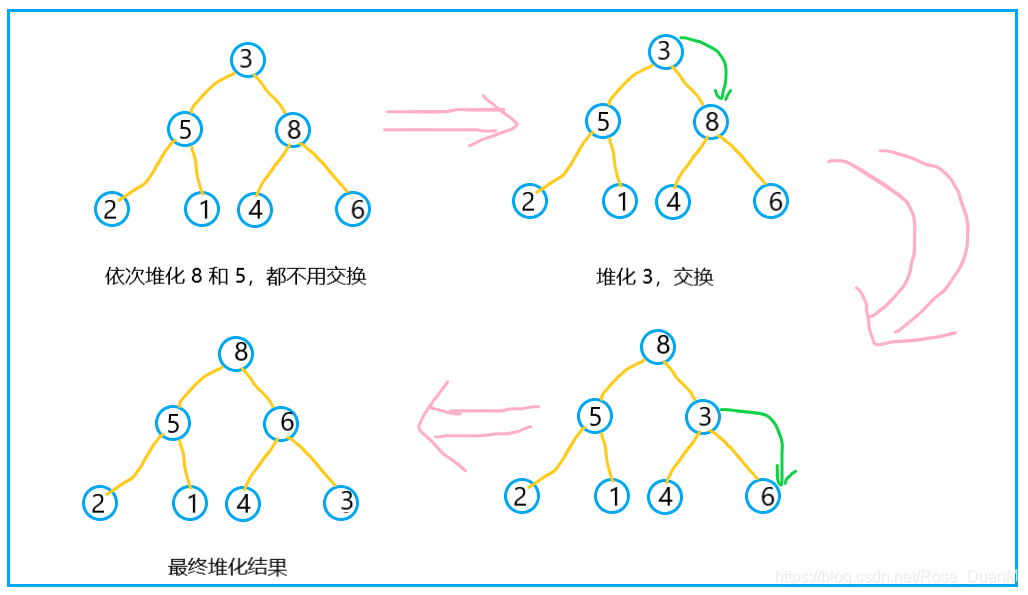
這樣，咱們就將一個無序的數組堆化成了具備堆的性質的數據，還須要說明如下，若是肯定一個堆的第一個非葉子節點是多少呢？實際上，對於長度爲 length 的數組，(length - 2) / 2下標對應的數據，就是堆中的第一個非葉子節點。接下來的操做就是排序了。

排序
排序的過程相似於上面說到的刪除堆頂元素，由於堆頂元素是堆的最大或最小元素，以大頂堆爲例，咱們只須要將堆頂元素和數組中最後一個元素交換位置，而後從新構造堆，繼續交換堆頂元素和數組中最後一個未排序數據，知道堆中元素剩下最後一個。

示意圖以下：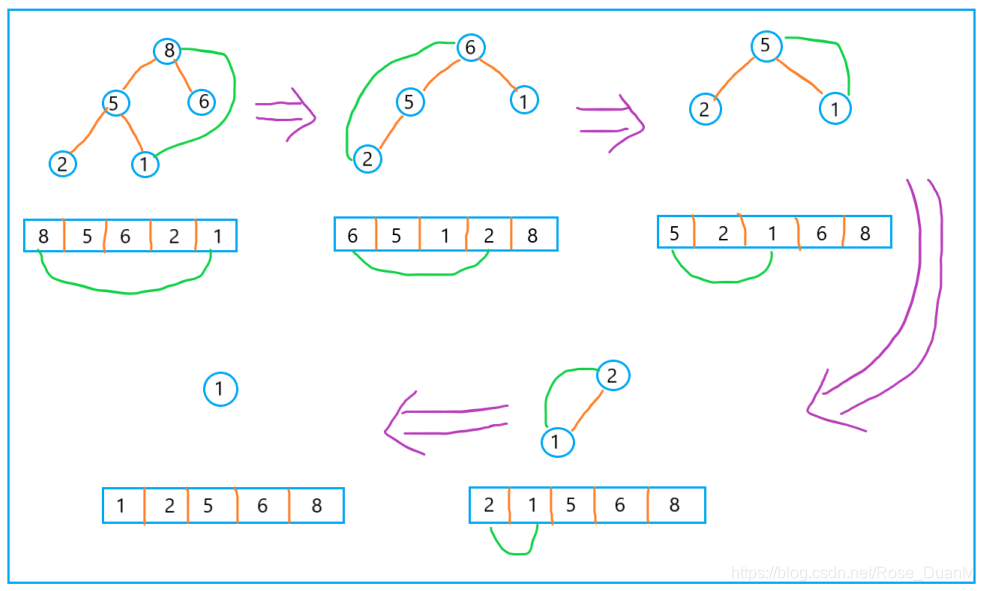

整個建堆和排序的實現的代碼也貼在這裏：

//堆排序
    public void heapSort(int[] data){
        int length = data.length;
        if (length <= 1) return;
        //建堆
        buildHeap(data);

        while (length > 0){
            swap(data, 0, --length);
            heapify(data, length, 0);
        }
    }
    //建堆
    //從非葉子節點依次堆化
    private void buildHeap(int[] data){
        int length = data.length;
        for (int i = (length - 2) / 2; i >= 0; -- i) {
            heapify(data, length, i);
        }
    }