深刻理解HashMap(一): 從源頭提及

前言

系列文章目錄

HashMap咱們都不陌生, 也是java面試幾乎必問的考點, 本系列咱們來深刻思考有關HashMap的設計思想和實現細節.

HashMap解決了什麼問題?

任何數據結構的產生總對應着要解決一個實際的問題, HashMap的產生要解決問題就是:

如何有效的 存 取 一組 key-vaule 鍵值對

key-value鍵值對是最常使用的數據形式, 如何有效地存取他們是衆多語言都須要關注的問題. 注意這裏有四個關鍵字:

1. key-value鍵值對
2. 一組
3. 存
4. 取

下面咱們逐個來思考:

如何表示 key-value 鍵值對

在java這種面向對象的語言中, 表示一個數據結構天然要用到類, 因爲對於鍵值對的數據類型事先並不清楚, 顯而易見這裏應該要用泛型, 則, 表示key-value鍵值對最簡單的形式能夠是:

class Node<K,V> {
    K key;
    V value;
}

這裏咱們自定義一個Node類, 它只有兩個屬性, 一個 key屬性表示鍵, 一個value屬性表示值, 則這個類就表明了一個 key-value鍵值對.

是否是很簡單?

固然, 咱們還須要定義一些方法來操縱這兩個屬性, 例如get和set方法等,不過根據設計原則, 咱們應該面向接口編程, 因此應該定義一個接口來描述須要執行的操做, 這個接口就是Entry<K,V>, 它只不過是對於Node<K,V>這個類的抽象, 在java中, 這個接口定義在Map這個接口中, 因此上面的類能夠改成:

class Node<K,V> implements Map.Entry<K,V>{
    K key;
    V value;
}

這裏咱們總結一下:

咱們定義了一個Node類來表示一個鍵值對, 爲了面向接口編程, 咱們抽象出一個 Entry接口, 並使Node類實現了這個接口.

至於這個接口須要定義哪些方法, 咱們暫不細表.

這樣, 到目前爲止, 咱們完成了對於 key-value 鍵值對的表示.

如何存儲 key-value 鍵值對的集合

在常見的業務邏輯中, 咱們經常須要處理一組鍵值對的集合, 將一組鍵值對存儲在一處, 並根據key值去查找對應的value.

那麼咱們要如何存儲這些鍵值對的集合呢?

其實換個問法可能更容易回答:

應該怎樣存儲一組對象?

(畢竟鍵值對已經被咱們表示爲Node對象了)

在java中, 存儲一個對象的集合無外乎兩種方式:

1. 數組
2. 鏈表

關於數組和鏈表的優缺點你們已經耳熟能詳了:

• 數組大小有限, 查找性能好, 插入和刪除性能差
• 鏈表大小不限, 查找性能差, 插入和刪除性能好

這裏應該選哪一種形式呢? 那得看實際的應用了, 在使用鍵值對時, 查找和插入,刪除等操做都會用到, 可是在實際的應用場景中, 對於鍵值對的查找操做居多, 因此咱們固然選擇數組形式.

Node<K,V>[] table;

總結: 咱們選擇數組形式來存儲key-value對象.

爲了便於下文描述, 咱們將數組的下標稱爲索引(index), 將數組中的一個存儲位置稱爲數組的一個存儲桶(bucket).

如何有效地根據key值查找value

前面已經講到, 咱們選擇數組形式來存儲key-value對象, 以利用其優良的查找性能, 數組之因此查找迅速, 是由於能夠根據索引(數組下標)直接定位到對應的存儲桶(數組所存儲對象的位置.)
可是實際應用中, 咱們都是經過key值來查找value值, 怎麼辦呢?

一種方式就是遍歷數組中的每個對象, 查看它的key是否是咱們要找的key, 可是很明顯, 這種方式效率低下(並且這不就是鏈表的順序查找方式嗎?) 徹底違背了咱們選擇數組來存儲鍵值對的初衷.

爲了利用索引來查找, 咱們須要創建一個 key -> index 的映射關係, 這樣每次咱們要查找一個 key時, 首先根據映射關係, 計算出對應的數組下標, 而後根據數組下標, 直接找到對應的key-value對象, 這樣基本能以o(1)的時間複雜度獲得結果.

這裏, 將key映射成index的方法稱爲hash算法, 咱們但願它能將 key均勻的分佈到數組中.

這裏插一句,使用Hash算法一樣補足了數組插入和刪除性能差的短板, 咱們知道, 數組之因此插入刪除性能差是由於它是順序存儲的, 在一個位置插入節點或者刪除節點須要一個個移動它的後續節點來騰出位或者覆蓋位置.

使用hash算法後, 數組再也不按順序存儲, 插入刪除操做只須要關注一個存儲桶便可, 而不須要額外的操做.

如何解決hash衝突

這個問題實際上是由上一個問題引出的, 雖然咱們要求hash算法能將key均勻的分佈到數組中, 可是它只能儘可能作到, 並非絕對的, 更況且咱們的數組大小是有限的, 保不齊咱們的hash算法將就兩個不一樣的key映射成了同一個index值, 這就產生了hash衝突, 也就是兩個Node要存儲在數組的同一個位置該怎麼辦?

解決hash衝突的方法有不少, 在HashMap中咱們選擇鏈地址法, 即在產生衝突的存儲桶中改成單鏈表存儲.(拓展閱讀: 解決哈希衝突的經常使用方法 )

其實, 最理想的效果是，Entry數組中每一個位置都只有一個元素，這樣，查詢的時候效率最高，不須要遍歷單鏈表，也不須要經過equals去比較Key，並且空間利用率最大。

鏈地址法使咱們的數組轉變成了鏈表的數組:

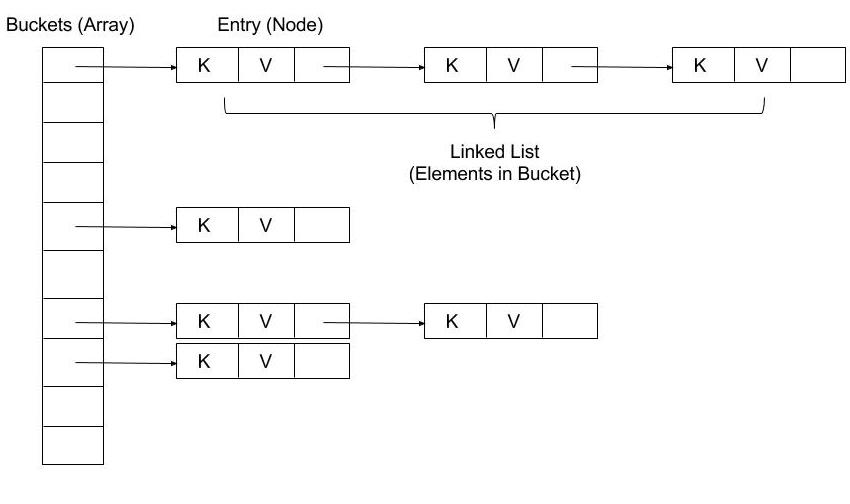
(圖片來自網絡)

至此, 咱們對key-value鍵值對的表示變爲:

class Node<K,V> implements Map.Entry<K,V> {
    final int hash;
    final K key;
    V value;
    Node<K,V> next;
    
    Node(int hash, K key, V value, Node<K,V> next) {
        this.hash = hash;
        this.key = key;
        this.value = value;
        this.next = next;
    }
    ...
}

鏈表長度過長怎麼辦

咱們知道, 鏈表查找只能經過順序查找來實現, 所以, 時間複雜度爲o(n), 若是很不巧, 咱們的key值被Hash算法映射到一個存儲桶上, 將會致使存儲桶上的鏈表長度愈來愈長, 此時, 數組查找退化成鏈表查找, 則時間複雜度由原來的o(1) 退化成 o(n).

爲了解決這一問題, 在java8中, 當鏈表長度超過 8 以後, 將會自動將鏈表轉換成紅黑樹, 以實現 o(log n) 的時間複雜度, 從而提高查找性能.

(圖片來自網絡)

何時擴容

前面已經說到, 數組的大小是有限的, 在新建的時候就要指定, 若是加入的節點已經到了數組容量的上限, 已經沒有位置可以存儲key-value鍵值對了, 此時就須要擴容.

可是很明顯, 咱們不會等到迫不及待了纔想起來要擴容, 在實際的應用中, 數組空間已使用3/4以後, 咱們就會括容.

爲何是0.75呢, 官方文檔的解釋是:

the default load factor (.75) offers a good tradeoff between time and space costs.

想要更深刻的理解能夠看這裏.

再說回擴容, 有的同窗就要問了, 咱上面不是將數組的每個元素轉變成鏈表了嗎? 就算此時節點數超過了數組大小, 新加的節點會存在數組某一個位置的鏈表裏啊, 鏈表的大小不限, 能夠存儲任意數量的節點啊!

沒錯, 理論上來講這樣確實是可行的, 但這又違背了咱們一開始使用數組來存儲一組鍵值對的初衷, 還記得咱們選擇數組的緣由是什麼嗎? 爲了利用索引快速的查找!

若是咱們試圖期望利用鏈表來擴容的話, 當一個存儲桶的中的鏈表愈來愈大, 在這個鏈表上的查找性能就會不好(退化成順序查找了)

爲此, 在數組容量不足時, 爲了繼續維持利用數組索引查找的優良性能, 咱們必須對數組進行擴容.

鏈表存在的意義只是爲了解決hash衝突, 而不是爲了增大容量. 事實上, 咱們但願鏈表的長度越短越好, 或者最好不要出現鏈表.

每次擴容擴多大

上一節咱們討論了擴容的時機, 接下來的另外一問題就是每次多增長多少空間.

咱們知道, 數組的擴容是一個很耗費CPU資源的動做, 須要將原數組的內容複製到新數組中去, 所以頻繁的擴容必然會致使性能下降, 因此不可能數組滿了以後, 每多加一個node, 咱們就擴容一次.
可是, 一次擴容太大, 致使大量的存儲空間用不完, 勢必又形成很大的浪費, 所以, 必須根據實際狀況設定一個合理的擴容大小.

在HashMap的實現中, 每次擴容咱們都會將新數組的大小設爲原數組大小的兩倍.

總結

關於HashMap的設計思路, 咱們能夠用一句話來歸納:

不忘初心 !

咱們設計HashMap的初心是什麼呢, 是找到一種方法, 能夠存儲一組鍵值對的集合, 並實現快速的查找.

==> 爲了實現快速查找, 咱們選擇了數組而不是鏈表. 以利用數組的索引實現o(1)複雜度的查找效率.

==> 爲了利用索引查找, 咱們引入Hash算法, 將 key 映射成數組下標: key -> Index

==> 引入Hash算法又致使了Hash衝突

==> 爲了解決Hash衝突, 咱們採用鏈地址法, 在衝突位置轉爲使用鏈表存儲.

==> 鏈表存儲過多的節點又致使了在鏈表上節點的查找性能的惡化

==> 爲了優化查找性能, 咱們在鏈表長度超過8以後轉而將鏈表轉變成紅黑樹, 以將 o(n)複雜度的查找效率提高至o(log n)

可見, 每一次結構的調整, 都是始終圍繞咱們的初心:

實現快速的查找

來進行的, 始終不忘這一點, 在每一次出現問題的時候, 一切的選擇是否是看起來就很天然了?(≧∇≦)ﾉ

(完)

下一篇: 深刻理解HashMap(二): 關鍵源碼逐行分析之hash算法

查看更多系列文章：系列文章目錄