前端該如何準備數據結構和算法？

時間 2019-11-05

標籤前端如何準備數據結構算法简体版

原文原文鏈接

1、導讀

據我瞭解，前端程序員有至關一部分對「數據結構」和「算法」的基礎概念都不是很清晰，這直接致使不少人在看到有關這部分的內容就會望而卻步。html

實際上，當你瞭解了「數據結構」和「算法」存在的真正意義，以及一些實際的應用場景，對它有了一個總體的認知以後，你可能會對它產生強烈的興趣。固然，它帶將帶給你的收益也是至關可觀的。前端

不少前端同窗在看到「數據結構」和「算法」後會有必定的抵觸心理，或者嘗試去練習，可是被難倒，從而放棄。git

這很大一部分緣由是由於你還不夠了解學習他們的意義，或者沒有掌握合理的練習方法。程序員

實際上，當你有了必定的目的性，而且有了合理的練習方法，再來學習這部份內容會變得駕輕就熟。
å
在本文中，我就來分享一下我學習「數據結構」和「算法」的一些經驗和方法。github

後面我也會針對全部常見的數據結構和算法分類，進行全方位的梳理。面試

1.1 類別說明

數據結構和算法的種類很是之多，拿樹舉例，樹的種類包括：二叉樹、B樹、B+樹、Trie樹、紅黑樹等等，本文只選擇了二叉樹。算法

對前端來說，沒有必要對某些比較偏的類型和解法多作了解，一是浪費寶貴的時間，二是應用的很少。編程

本文選擇的數據結構和算法的類別均是出現頻率最高，以及應用最廣的類別。segmentfault

1.2 題目說明

另外，作題時找對典型題目很是重要，可讓你更快速更高效的掌握知識，本文後面也會給出每種類型的典型題目供你們參考。數組

題目來源：

awesome-coding-js：個人前端算法開源項目，包括我作過的題目以及詳細解析
leetcode
劍指offer

另外，我會在後面長期更新一個前端算法的專欄，對每類數據結構和算法進行詳細的講解，敬請期待。

2、爲何要學習數據結構和算法

在學習某塊內容以前，咱們必定要首先明確爲何要學，而不是盲目的跟風。

這將更有利於你從學習的過程當中得到收益，並且會爲你的學習帶來動力。

首先明確一點，學習數據結構和算法不必定就是記住二叉樹、堆、棧、隊列等的解題方法也不是死記硬背一些題目，若是你僅僅停留在這樣的表面思想，那麼你學習起來會很是痛苦。

2.1 解決問題的思想

計算機只是一個很冰冷的機器，你給他下發什麼樣的指令，它就能做出什麼樣的反應。

而開發工程師要作的是如何把實際的問題轉化成計算機的指令，如何轉化，來看看《數據結構》的經典說法：

設計出數據結構，在施加以算法就好了。

因此，很重要的一點，數據結構和算法對創建解決問題的思想很是重要。

若是說 Java 是自動檔轎車，C 就是手動檔吉普。數據結構呢？是變速箱的工做原理。你徹底能夠不知道變速箱怎樣工做，就把自動檔的車子從 A 開到 B，並且未必就比懂得的人慢。寫程序這件事，和開車同樣，經驗能夠起到很大做用，但若是你不知道底層是怎麼工做的，就永遠只能開車，既不會修車，也不能造車。若是你對這兩件事都不感興趣也就罷了，數據結構懂得用就好。但若你今生在編程領域還有點更高的追求，數據結構是繞不開的課題。

2.2 面試

這是很是現實的一點，也是不少前端學習數據結構和算法的緣由。

通常對待算法的態度會分爲如下幾類：

Google、Microsoft等知名外企在面試工程師時，算法是起決定性因素的，前端工程師也是同樣，基本是每一輪都會考察，即便你有很是強的背景，也有可能由於一兩道算法答的很差而與這樣的企業失之交臂。

第二類，算法佔重要因素的，國內的某些大廠在面試時，也會把數據結構和算法做爲重要的參考因素，基本是面試必考，若是你達不到必定的要求，會直接掛掉。

第三類，起加分做用，不少公司不會把數據結構和算法做爲硬性要求，可是也會象徵性的出一些題目，當你把一道算法題答的很漂亮，這絕對是加分項。

可見，學好數據結構和算法對你跳槽更好的公司或者拿到更高的薪水，是很是重要的。

3、如何準備

瞭解了數據結構和算法的重要性，那麼究竟該用什麼樣的方法去準備呢？

3.1 全方位瞭解

在學習和練習以前，你必定要對數據結構和算法作一個全方位的瞭解，對數據結構和算法的定義、分類作一個全面的理解，若是這部分作的很差，你在作題時將徹底不知道你在作什麼，從而陷入盲目尋找答案的過程，這個過程很是痛苦，並且每每收益甚微。

本文後面的章節，我會對常見的數據結構和算法作一個全方位的梳理。

3.2 分類練習

當你對數據結構和算法有了一個總體的認知以後，就能夠開始練習了。

注意，必定是分類練習！分類練習！分類練習！重要的事情說三遍。

我曾見過很是多的同窗帶着一腔熱血就開始刷題了，從leetcode第一題開始，剛開始每每很是有動力，可能還會發個朋友圈或者沸點什麼的😅，而後就沒有而後了。

由於前幾題很是簡單，可能會給你必定的自信，可是，按序號來的話，很快就會遇到hard。或者有的人，乾脆只刷簡單，先把全部的簡單刷完。

可是，這樣盲目的刷題，效果是很是差的，有可能你堅持下來，刷了幾百道，也能有點效果，可是整個過程可能很是慢，並且效果遠遠沒有分類練習要好。

所謂分類練習，即按每種類別練習，例如：這段時間只練習二叉樹的題目，後面開始練習回溯算法的題目。

在開始練習以前，你每每還須要對這種具體的類別進行一個詳細的瞭解，對其具體的定義、相關的概念和應用、可能出現的題目類型進行梳理，而後再開始。

3.3 按期回顧和總結

在對一個類型針對練習一些題目以後，你就能夠發現必定的規律，某一些題目是這樣解，另外一些題目是那樣解...這是一個很正常的現象，每種類型的題目確定是存在必定規律的。

這時候就能夠開始對此類題目進行總結了，針對此類問題，以及其典型的題目，發現的解題方法，進行總結。當下次你再遇到這種類型的題目，你就能很快想到解題思路，從而很快的解答。

因此，當你看到一個題目，首先你要想到它屬於哪一種數據結構或算法，而後要想到這是一個什麼類型的問題，而後是此類問題的解決方法。

若是你看到一個新的問題還不能作到上面這樣，那說明你對此類題目的掌握程度還不夠，你還要多花一些經從來進行練習。

固然，後面我會把我在這部分的總結分享出來，幫助你們少走一些彎路。

3.4 題目的選擇

關於題目來源，這裏我推薦先看《劍指offer》，而後是leetcode，《劍指offer》上能找到很是多的典型題目，這對你發現和總結規律很是重要。看完再去刷leetcode你會發現更加輕鬆。

關於難度的選擇，這裏我建議leetcode簡單、中等難度便可，由於咱們要作的是尋找規律，即掌握典型題目便可，當你掌握了這些規律，再去解一些hard的問題，也是能夠的，只是多花些時間的問題。切忌不要一開始就在不少刁鑽古怪的問題上耗費太多時間。

通過上面的方法，我在練習一段時間後，基本leetcode中等難度的問題能夠在20min內AC，另外在最近跳槽的過程當中，基本全部的算法問題我都能很快的手寫出來，或者很快的想到解題思路。但願你們在看到個人經驗和方法後也能達到這樣的效果，或者作的比我更好。

4、時間複雜度和空間複雜度

在開始學習以前，咱們首先要搞懂時間複雜度和空間複雜度的概念，它們的高低共同決定着一段代碼質量的好壞：

4.1 時間複雜度

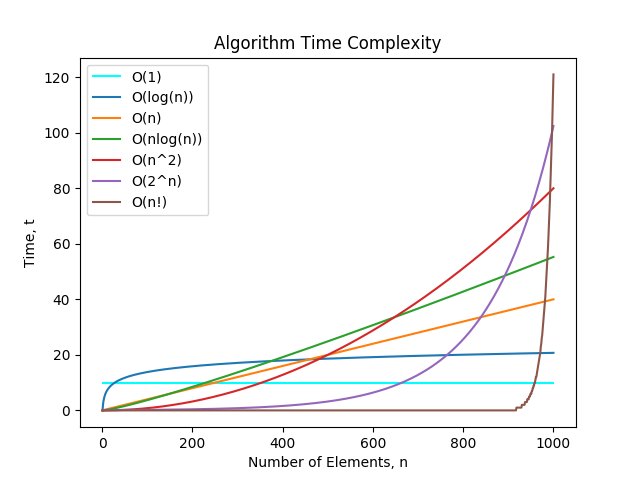
一個算法的時間複雜度反映了程序運行從開始到結束所須要的時間。把算法中基本操做重複執行的次數（頻度）做爲算法的時間複雜度。

沒有循環語句，記做O(1)，也稱爲常數階。只有一重循環，則算法的基本操做的執行頻度與問題規模n呈線性增大關係，記做O（n），也叫線性階。

常見的時間複雜度有：

O(1): Constant Complexity: Constant 常數複雜度
O(log n): Logarithmic Complexity: 對數複雜度
O(n): Linear Complexity: 線性時間複雜度
O(n^2): N square Complexity 平⽅方
O(n^3): N square Complexity ⽴立⽅方
O(2^n): Exponential Growth 指數
O(n!): Factorial 階乘

4.2 空間複雜度

一個程序的空間複雜度是指運行完一個程序所需內存的大小。利用程序的空間複雜度，能夠對程序的運行所須要的內存多少有個預先估計。

一個程序執行時除了須要存儲空間和存儲自己所使用的指令、常數、變量和輸入數據外，還須要一些對數據進行操做的工做單元和存儲一些爲現實計算所需信息的輔助空間。

5、數據結構

數據結構這個詞相信你們都不陌生，在不少場景下可能都聽過，但你有沒有考慮過「數據結構」到底是一個什麼東西呢？

數據結構即數據元素相互之間存在的一種和多種特定的關係集合。

通常你能夠從兩個維度來理解它，邏輯結構和存儲結構。

5.1 邏輯結構

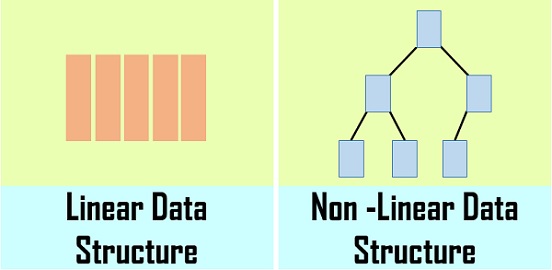
簡單的來講邏輯結構就是數據之間的關係，邏輯結構大概統一的能夠分紅兩種：線性結構、非線性結構。

線性結構：是一個有序數據元素的集合。其中數據元素之間的關係是一對一的關係，即除了第一個和最後一個數據元素以外，其它數據元素都是首尾相接的。

經常使用的線性結構有: 棧，隊列，鏈表，線性表。

—非線性結構：各個數據元素再也不保持在一個線性序列中，每一個數據元素可能與零個或者多個其餘數據元素髮生聯繫。

常見的非線性結構有二維數組，樹等。

5.2 存儲結構

邏輯結構指的是數據間的關係，而存儲結構是邏輯結構用計算機語言的實現。常見的存儲結構有順序存儲、鏈式存儲、索引存儲以及散列存儲。

例如：數組在內存中的位置是連續的，它就屬於順序存儲；鏈表是主動創建數據間的關聯關係的，在內存中卻不必定是連續的，它屬於鏈式存儲；還有順序和邏輯上都不存在順序關係，可是你能夠經過必定的方式去放問它的哈希表，數據散列存儲。

5.3 數據結構-二叉樹

樹是用來模擬具備樹狀結構性質的數據集合。根據它的特性能夠分爲很是多的種類，對於咱們來說，掌握二叉樹這種結構就足夠了，它也是樹最簡單、應用最普遍的種類。

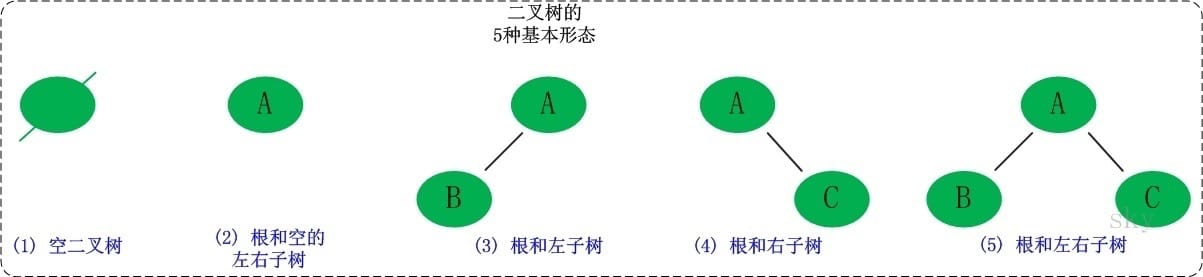
二叉樹是一種典型的樹樹狀結構。如它名字所描述的那樣，二叉樹是每一個節點最多有兩個子樹的樹結構，一般子樹被稱做「左子樹」和「右子樹」。

5.3.1 二叉樹遍歷

重點中的重點，最好同時掌握遞歸和非遞歸版本，遞歸版本很容易書寫，可是真正考察基本功的是非遞歸版本。

根據前序遍歷和中序遍歷的特色重建二叉樹，逆向思惟，頗有意思的題目

5.3.2 二叉樹的對稱性

5.3.3 二叉搜索樹

二叉搜索樹是特殊的二叉樹，考察二叉搜索樹的題目通常都是考察二叉搜索樹的特性，因此掌握好它的特性很重要。

若任意節點的左⼦子樹不不空，則左⼦子樹上全部結點的值均⼩小於它的根結點的值;
若任意節點的右⼦子樹不不空，則右⼦子樹上全部結點的值均⼤大於它的根結點的值;
任意節點的左、右⼦子樹也分別爲⼆二叉查找樹。

5.3.4 二叉樹的深度

二叉樹的深度爲根節點到最遠葉子節點的最長路徑上的節點數。
平衡二叉樹：左右子樹深度之差大於1

5.4 數據結構-鏈表

用一組任意存儲的單元來存儲線性表的數據元素。一個對象存儲着自己的值和下一個元素的地址。

須要遍歷才能查詢到元素，查詢慢。
插入元素只需斷開鏈接從新賦值，插入快。

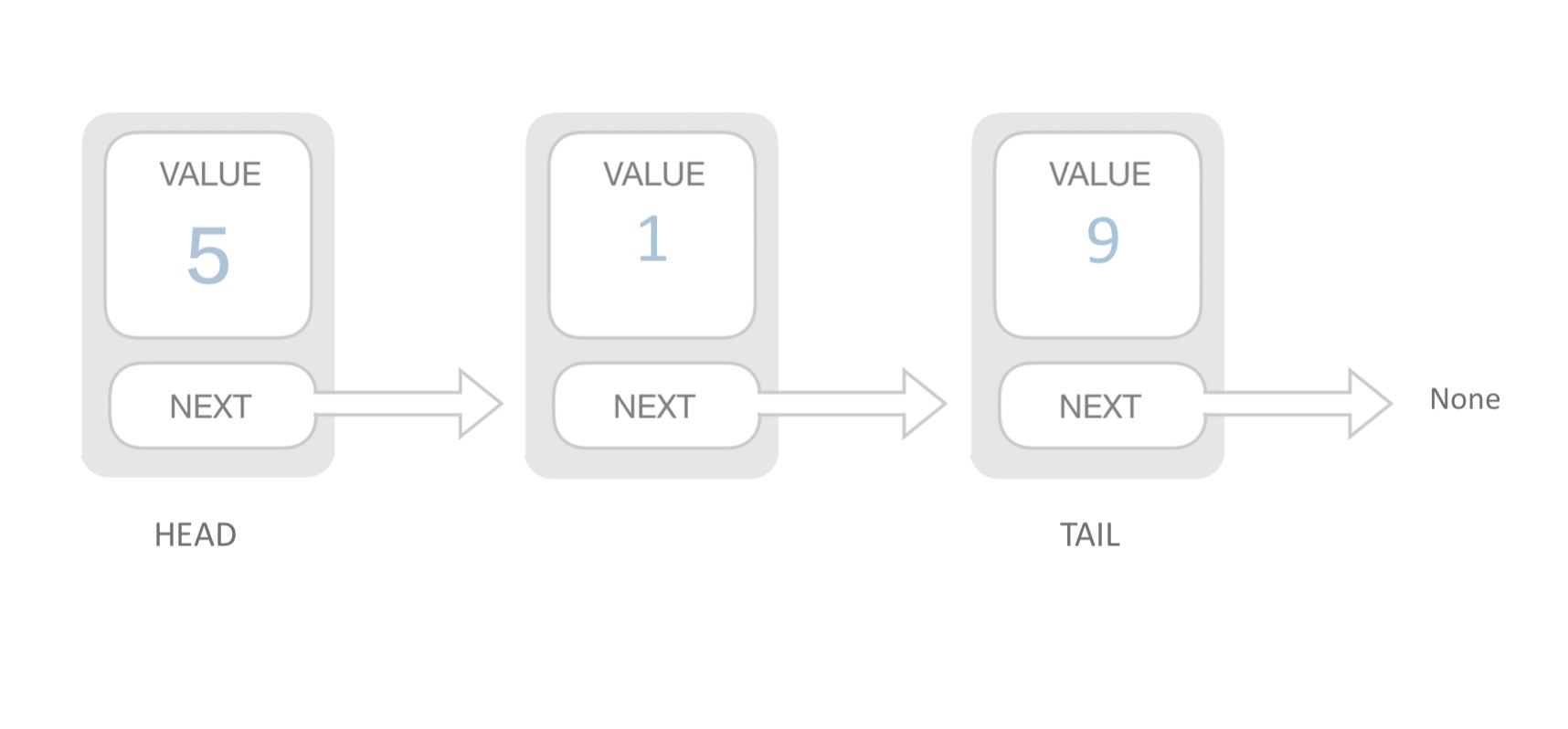
鏈表在開發中也是常常用到的數據結構，React16的 Fiber Node鏈接起來造成的Fiber Tree, 就是個單鏈表結構。

5.4.1 基本應用

主要是對鏈表基本概念和特性的應用，若是基礎概念掌握牢靠，此類問題便可迎刃而解

5.4.2 環類題目

環類題目即從判斷一個單鏈表是否存在循環而擴展衍生的問題

5.4.3 雙指針

雙指針的思想在鏈表和數組中的題目都常常會用到，主要是利用兩個或多個不一樣位置的指針，經過速度和方向的變換解決問題。

兩個指針從不一樣位置出發：一個從始端開始，另外一個從末端開始；
兩個指針以不一樣速度移動：一個指針快一些，另外一個指針慢一些。

對於單鏈表，由於咱們只能在一個方向上遍歷鏈表，因此第一種情景可能沒法工做。然而，第二種情景，也被稱爲慢指針和快指針技巧，是很是有用的。

5.4.4 雙向鏈表

雙鏈還有一個引用字段，稱爲prev字段。有了這個額外的字段，您就可以知道當前結點的前一個結點。

扁平化多級雙向鏈表

5.5 數據結構-數組

數組是咱們在開發中最多見到的數據結構了，用於按順序存儲元素的集合。可是元素能夠隨機存取，由於數組中的每一個元素均可以經過數組索引來識別。插入和刪除時要移動後續元素，還要考慮擴容問題，插入慢。

數組與平常的業務開發聯繫很是緊密，如何巧妙的用好數組是咱們可否開發出高質量代碼的關鍵。

5.5.1 雙指針

上面鏈表中提到的一類題目，主要是利用兩個或多個不一樣位置的指針，經過速度和方向的變換解決問題。注意這種技巧常常在排序數組中使用。

5.5.2 N數之和問題

很是常見的問題，基本上都是一個套路，主要考慮如何比暴利法下降時間複雜度，並且也會用到上面的雙指針技巧

5.5.3 二維數組

創建必定的抽象建模能力，將實際中的不少問題進行抽象

5.5.4 數據統計

數組少不了的就是統計和計算，此類問題考察如何用更高效的方法對數組進行統計計算。

5.6 數據結構-棧和隊列

在上面的數組中，咱們能夠經過索引隨機訪問元素，可是在某些狀況下，咱們可能要限制數據的訪問順序，因而有了兩種限制訪問順序的數據結構：棧（後進後出）、隊列（先進先出）

5.7 數據結構-哈希表

哈希的基本原理是將給定的鍵值轉換爲偏移地址來檢索記錄。

鍵轉換爲地址是經過一種關係（公式）來完成的，這就是哈希（散列）函數。

雖然哈希表是一種有效的搜索技術，可是它還有些缺點。兩個不一樣的關鍵字，因爲哈希函數值相同，於是被映射到同一表位置上。該現象稱爲衝突。發生衝突的兩個關鍵字稱爲該哈希函數的同義詞。

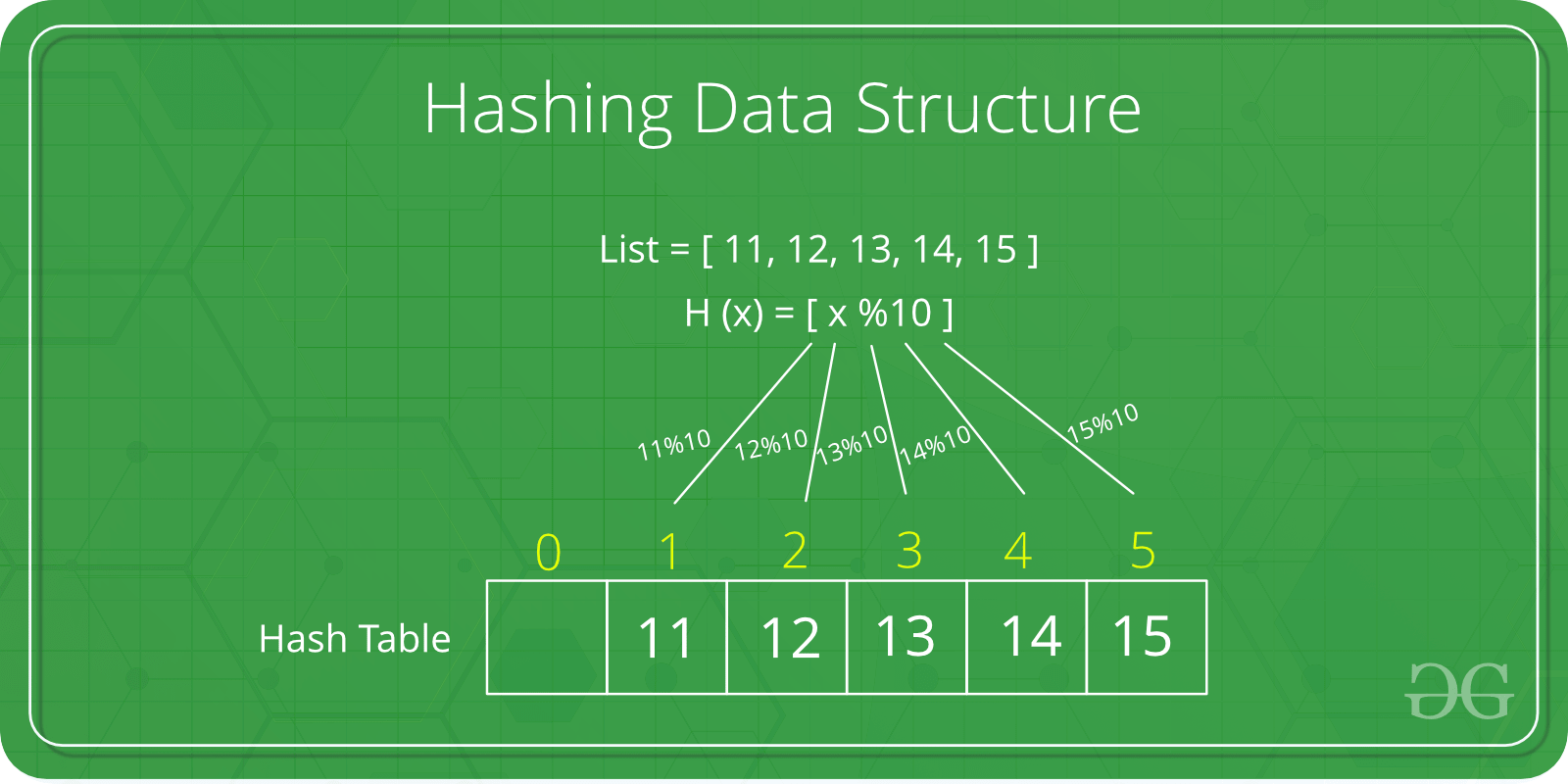
如何設計哈希函數以及如何避免衝突就是哈希表的常見問題。
好的哈希函數的選擇有兩條標準：

1.簡單而且可以快速計算
2.可以在址空間中獲取鍵的均勻人分佈

例以下面的題目：

常數時間插入、刪除和獲取隨機元素

當用到哈希表時咱們一般是要開闢一個額外空間來記錄一些計算過的值，同時咱們又要在下一次計算的過程當中快速檢索到它們，例如上面提到的兩數之和、三數之和等都利用了這種思想。

5.8 數據結構-堆

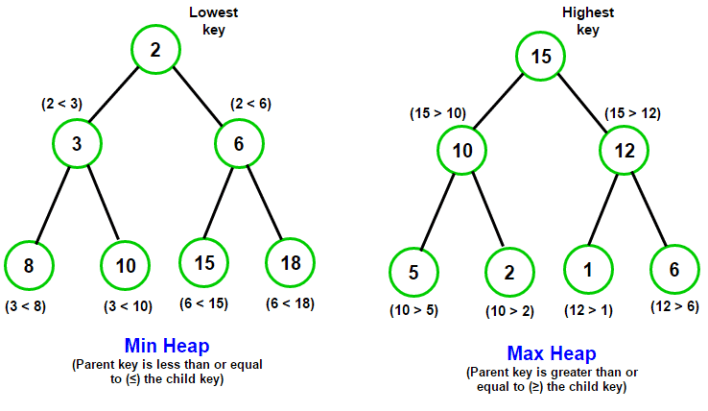
堆的底層其實是一棵徹底二叉樹，能夠用數組實現

每一個的節點元素值不小於其子節點 - 最大堆
每一個的節點元素值不大於其子節點 - 最小堆

堆在處理某些特殊場景時能夠大大下降代碼的時間複雜度，例如在龐大的數據中找到最大的幾個數或者最小的幾個數，能夠藉助堆來完成這個過程。

6、算法

6.1 排序

排序或許是前端接觸最多的算法了，不少人的算法之路是從一個冒泡排序開始的，排序的方法有很是多中，它們各自有各自的應用場景和優缺點，這裏我推薦以下6種應用最多的排序方法，若是你有興趣也能夠研究下其餘幾種。

快速排序

選擇一個目標值，比目標值小的放左邊，比目標值大的放右邊，目標值的位置已排好，將左右兩側再進行快排。

歸併排序

將大序列二分紅小序列，將小序列排序後再將排序後的小序列歸併成大序列。

選擇排序

每次排序取一個最大或最小的數字放到前面的有序序列中。

插入排序

將左側序列當作一個有序序列，每次將一個數字插入該有序序列。插入時，從有序序列最右側開始比較，若比較的數較大，後移一位。

冒泡排序

循環數組，比較當前元素和下一個元素，若是當前元素比下一個元素大，向上冒泡。下一次循環繼續上面的操做，不循環已經排序好的數。

堆排序

建立一個大頂堆，大頂堆的堆頂必定是最大的元素。交換第一個元素和最後一個元素，讓剩餘的元素繼續調整爲大頂堆。從後往前以此和第一個元素交換並從新構建，排序完成。

6.2 二分查找

查找是計算機中最基本也是最有用的算法之一。它描述了在有序集合中搜索特定值的過程。

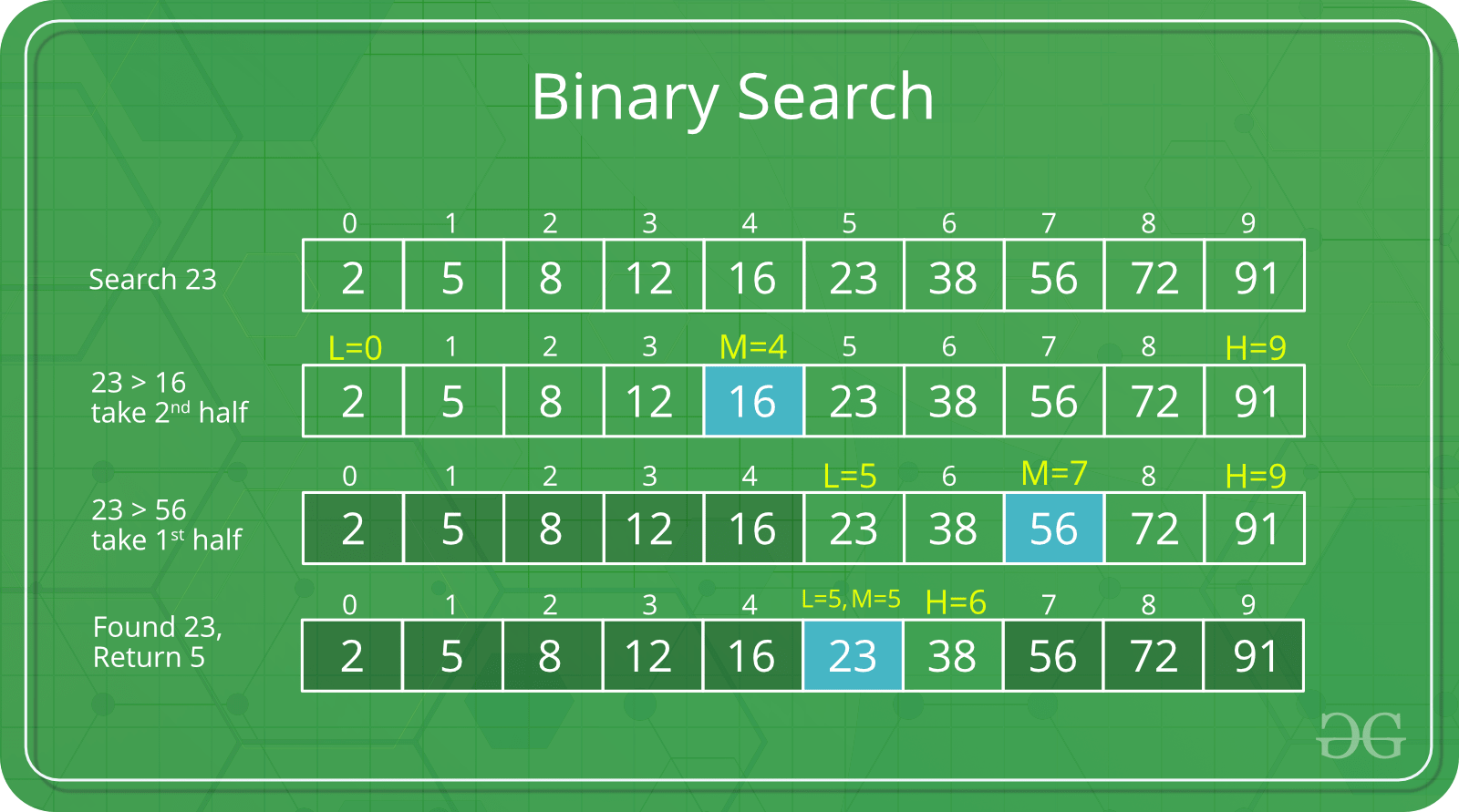
二分查找維護查找空間的左、右和中間指示符，並比較查找目標或將查找條件應用於集合的中間值；若是條件不知足或值不相等，則清除目標不可能存在的那一半，並在剩下的一半上繼續查找，直到成功爲止。若是查以空的一半結束，則沒法知足條件，而且沒法找到目標。

6.3 遞歸

遞歸是一種解決問題的有效方法，在遞歸過程當中，函數將自身做爲子例程調用。

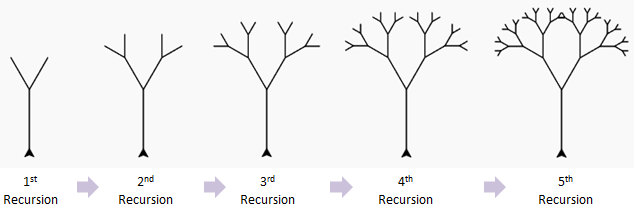
你可能想知道如何實現調用自身的函數。訣竅在於，每當遞歸函數調用自身時，它都會將給定的問題拆解爲子問題。遞歸調用繼續進行，直到到子問題無需進一步遞歸就能夠解決的地步。

爲了確保遞歸函數不會致使無限循環，它應具備如下屬性：

一個簡單的基本案例 —— 可以不使用遞歸來產生答案的終止方案。
一組規則，也稱做遞推關係，可將全部其餘狀況拆分到基本案例。

6.3.1 重複計算

一些問題使用遞歸考慮，思路是很是清晰的，可是卻不推薦使用遞歸，例以下面的幾個問題：

這幾個問題使用遞歸都有一個共同的缺點，那就是包含大量的重複計算，若是遞歸層次比較深的話，直接會致使JS進程崩潰。

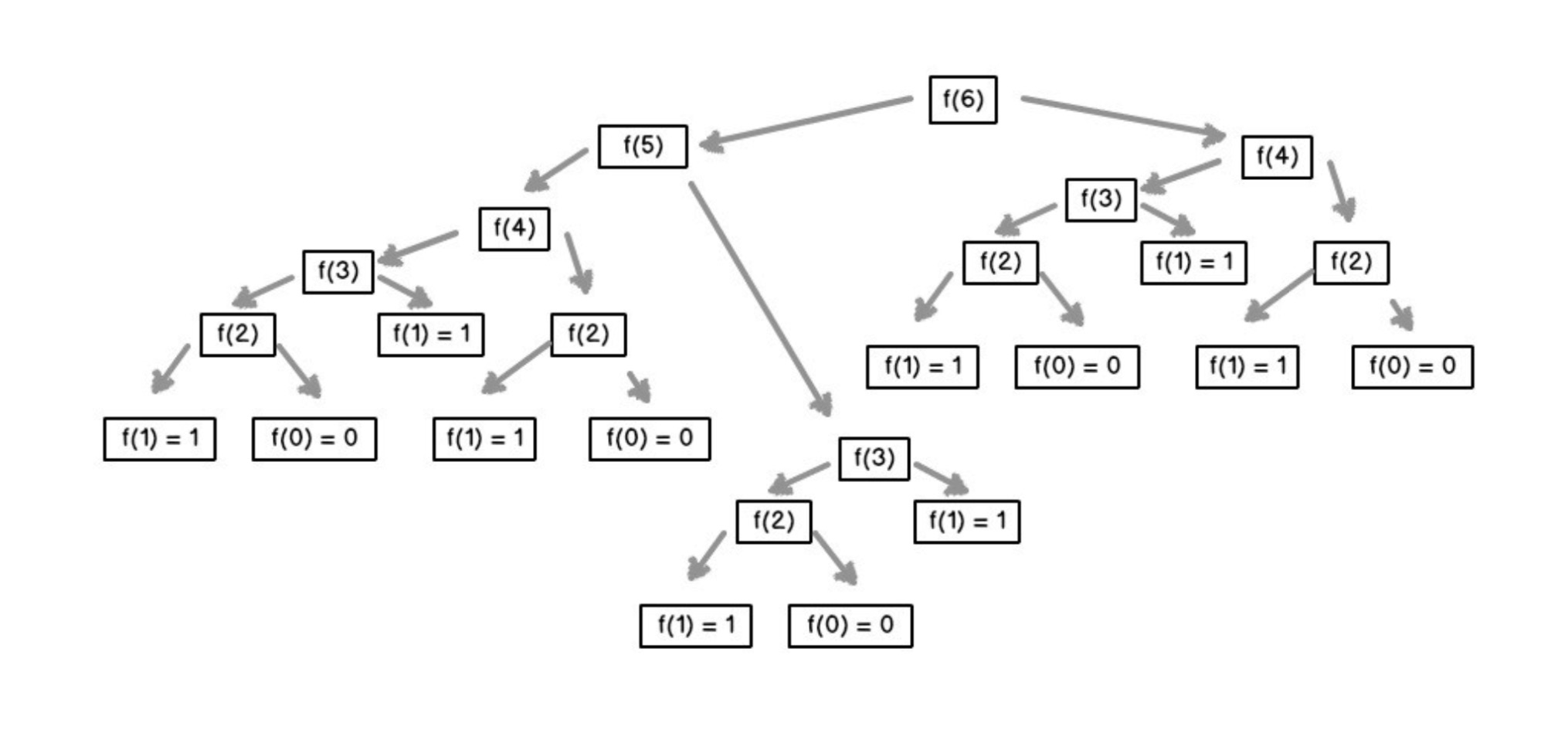
你可使用記憶化的方法來避免重複計算，即開闢一個額外空間來存儲已經計算過的值，可是這樣又會浪費必定的內存空間。所以上面的問題通常會使用動態規劃求解。

因此，在使用遞歸以前，必定要判斷代碼是否含有重複計算，若是有的話，不推薦使用遞歸。

遞歸是一種思想，而非一個類型，不少經典算法都是以遞歸爲基礎，所以這裏就再也不給出更多問題。

6.4 廣度優先搜索

廣度優先搜索（BFS）是一種遍歷或搜索數據結構（如樹或圖）的算法，也能夠在更抽象的場景中使用。

它的特色是越是接近根結點的結點將越早地遍歷。

例如，咱們可使用 BFS 找到從起始結點到目標結點的路徑，特別是最短路徑。

在BFS中，結點的處理順序與它們添加到隊列的順序是徹底相同的順序，即先進先出，因此廣度優先搜索通常使用隊列實現。

6.5 深度優先搜索

和廣度優先搜索同樣，深度優先搜索（DFS）是用於在樹/圖中遍歷/搜索的一種重要算法。

與 BFS 不一樣，更早訪問的結點可能不是更靠近根結點的結點。所以，你在DFS 中找到的第一條路徑可能不是最短路徑。

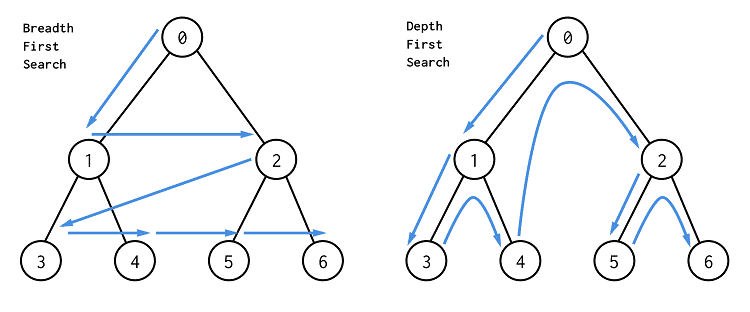
在DFS中，結點的處理順序是徹底相反的順序，就像它們被添加到棧中同樣，它是後進先出。因此深度優先搜索通常使用棧實現。

6.6 回溯算法

從解決問題每一步的全部可能選項裏系統選擇出一個可行的解決方案。

在某一步選擇一個選項後，進入下一步，而後面臨新的選項。重複選擇，直至達到最終狀態。

回溯法解決的問題的全部選項能夠用樹狀結構表示。

在某一步有n個可能的選項，該步驟可看做樹中一個節點。
節點每一個選項當作節點連線，到達它的n個子節點。
葉節點對應終結狀態。
葉節點知足約束條件，則爲一個可行的解決方案。
葉節點不知足約束條件，回溯到上一個節點，並嘗試其餘葉子節點。
節點全部子節點均不知足條件，再回溯到上一個節點。
全部狀態均不能知足條件，問題無解。

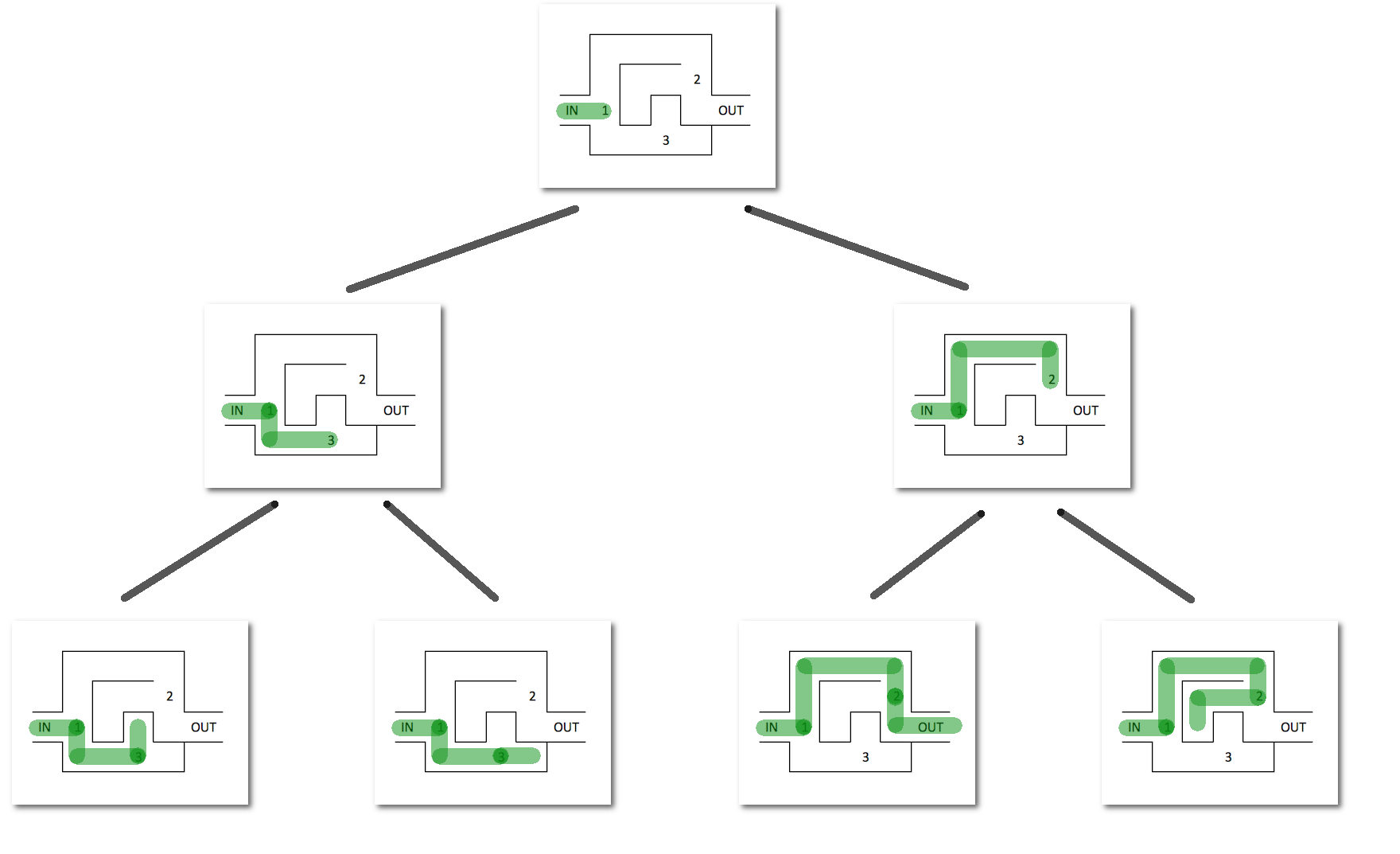
回溯算法適合由多個步驟組成的問題，而且每一個步驟都有多個選項。

6.7 動態規劃

動態規劃每每是最能有效考察算法和設計能力的題目類型，面對這類題目最重要的是抓住問題的階段，瞭解每一個階段的狀態，從而分析階段之間的關係轉化。

適用於動態規劃的問題，須要知足最優子結構和無後效性，動態規劃的求解過程，在於找到狀態轉移方程，進行自底向上的求解。

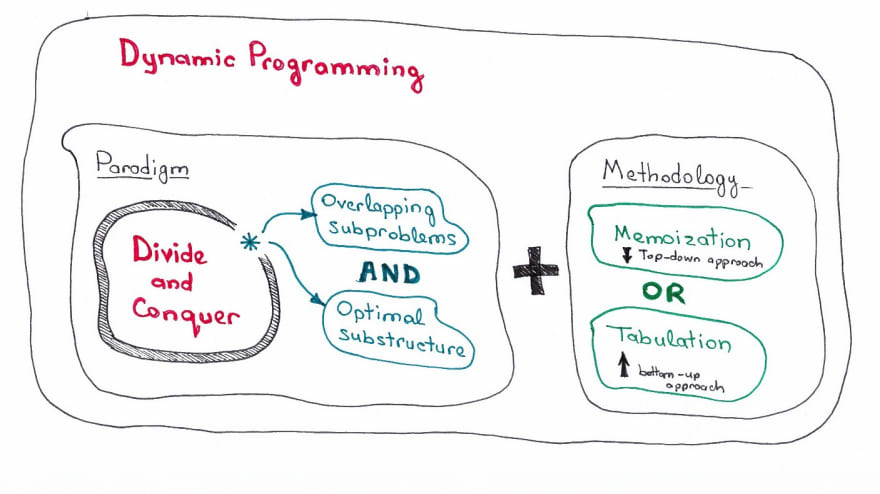
自底向上的求解，能夠幫你省略大量的複雜計算，例如上面的斐波拉契數列，使用遞歸的話時間複雜度會呈指數型增加，而動態規劃則讓此算法的時間複雜度保持在O(n)。

6.7.1 路徑問題

6.7.2 買賣股票類問題

子序列問題

6.8 貪心算法

貪心算法：對問題求解的時候，老是作出在當前看來是最好的作法。

適用貪心算法的場景：問題可以分解成子問題來解決，子問題的最優解能遞推到最終問題的最優解。這種子問題最優解成爲最優子結構

6.8.1 買賣股票類問題

6.8.2 貨幣選擇問題

6.9 貪心算法、動態規劃、回溯的區別

貪心算法與動態規劃的不一樣在於它對每一個子問題的解決方案都做出選擇，不能回退，動態規劃則會保存之前的運算結果，並根據之前的結果對當前進行選擇，有回退功能，而回溯算法就是大量的重複計算來得到最優解。

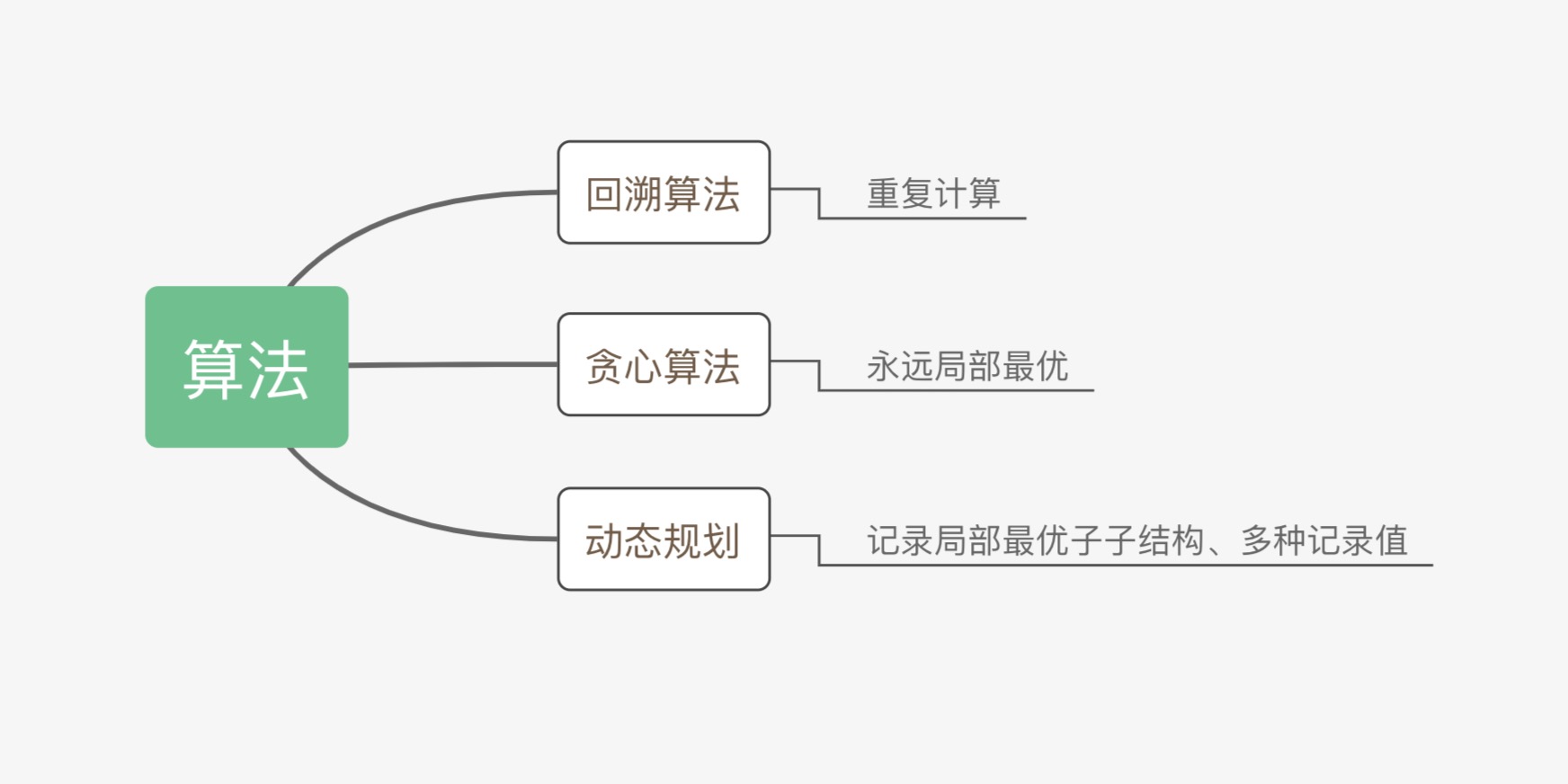
有不少算法題目都是能夠用這三種思想同時解答的，可是總有一種最適合的解法，這就須要不斷的練習和總結來進行深刻的理解才能更好的選擇解決辦法。

7、前端編碼能力

這部分是與前端開發貼近最緊密的一部分了，在寫業務代碼的同時，咱們也應該關心一些類庫或框架的內部實現。

大多數狀況下，咱們在寫業務的時候不須要手動實現這些輪子，可是它們很是考察一個前端程序員的編碼功底，若是你有必定的算法和數據結構基礎，不少源碼看起來就很是簡單。

下面我揀選了一些問題：

8、小結

本文的部分圖片來源於網絡，若有侵權，請聯繫我刪除，謝謝。

本文並無對每一個點進行深刻的分析，而是從爲何、怎麼作、作什麼的角度對數據結構和算法進行的全面分析（針對前端角度），但願看完本片文章能對你有以下幫助：

對數據結構和算法創建一個較全面的認知體系
掌握快速學習數據結構和算法的方法
瞭解數據結構和算法的重要分類和經典題型

若是你還想更深刻的學習數據結構和算法，請關注個人後續文章。

推薦個人算法總結：awesome-coding-js：https://github.com/ConardLi/a...

文中若有錯誤，歡迎在評論區指正，若是這篇文章幫助到了你，歡迎點贊和關注。

想閱讀更多優質文章、可關注個人github博客，你的star✨、點贊和關注是我持續創做的動力！

推薦關注個人微信公衆號【code祕密花園】，天天推送高質量文章，咱們一塊兒交流成長。

相關標籤/搜索

每日一句

每一个你不满意的现在，都有一个你没有努力的曾经。