二分類、多分類與多標籤問題的區別,對應損失函數的選擇,你知道嗎？

時間 2019-12-04

原文原文鏈接

二分類、多分類與多標籤分類問題使用不一樣的激活函數和損失函數，結論見文末總結（若是你趕時間能夠直接看結論，但建議有時間時回過頭來看看分析更有助於理解）。git

更多人工智能基礎知識見望江小車車的博客github

二分類、多分類與多標籤的基本概念

二分類：表示分類任務中有兩個類別，好比咱們想識別一幅圖片是否是貓。也就是說，訓練一個分類器，輸入一幅圖片，用特徵向量x表示，輸出是否是貓，用y=0或1表示。二類分類是假設每一個樣本都被設置了一個且僅有一個標籤 0 或者 1。算法

多類分類(Multiclass classification): 表示分類任務中有多個類別, 好比對一堆水果圖片分類, 它們多是橘子、蘋果、梨等. 多類分類是假設每一個樣本都被設置了一個且僅有一個標籤: 一個水果能夠是蘋果或者梨, 可是同時不多是二者。網絡

多標籤分類(Multilabel classification): 給每一個樣本一系列的目標標籤. 能夠想象成一個數據點的各屬性不是相互排斥的(一個水果既是蘋果又是梨就是相互排斥的), 好比一個文檔相關的話題. 一個文本可能被同時認爲是宗教、政治、金融或者教育相關話題。ide

多分類問題與二分類問題關係

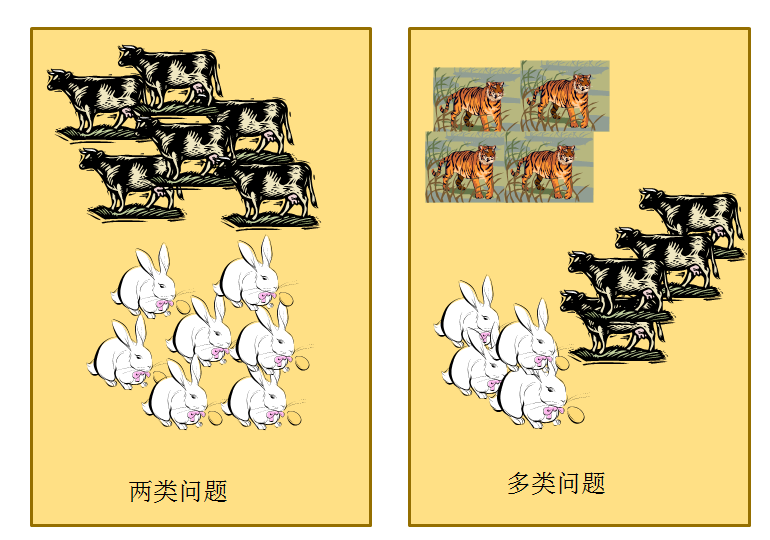
首先，兩類問題是分類問題中最簡單的一種。其次，不少多類問題能夠被分解爲多個兩類問題進行求解（請看下文分解）。因此，歷史上有不少算法都是針對兩類問題提出的。下面咱們來分析如何處理多分類問題：函數

直接分紅多類

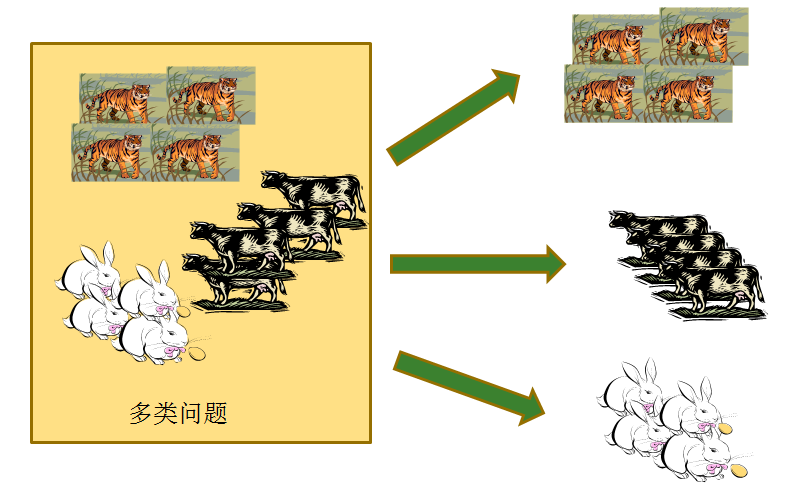
一對一的策略

給定數據集D這裏有N個類別，這種狀況下就是將這些類別兩兩配對，從而產生N(N−1)2個二分類任務，在測試的時候把樣本交給這些分類器，而後進行投票。測試

一對其他策略

將每一次的一個類做爲正例，其他做爲反例，總共訓練N個分類器。測試的時候若僅有一個分類器預測爲正的類別則對應的類別標記做爲最終分類結果，如有多個分類器預測爲正類，則選擇置信度最大的類別做爲最終分類結果。ui

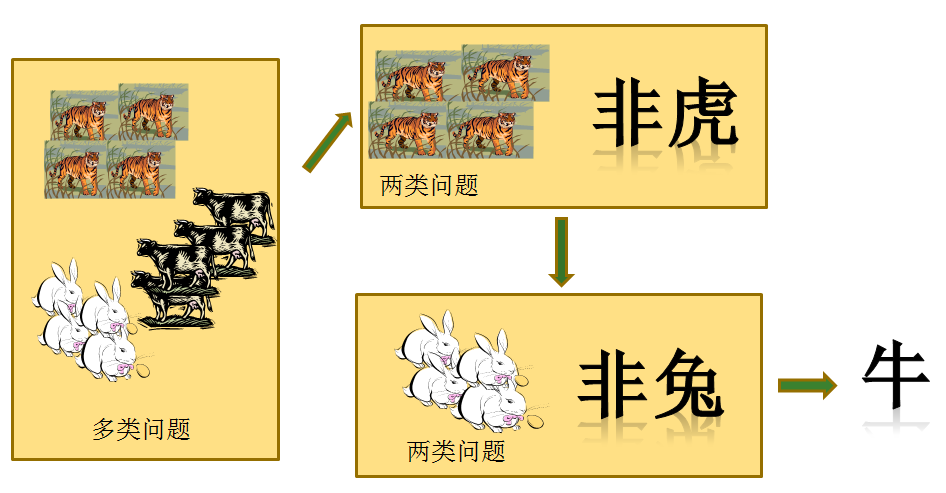
多標籤問題與二分類問題關係

面臨的問題： 圖片的標籤數目不是固定的，有的有一個標籤，有的有兩個標籤，但標籤的種類總數是固定的，好比爲5類。編碼

解決該問題： 採用了標籤補齊的方法，即缺失的標籤所有使用0標記，這意味着，再也不使用one-hot編碼。例如：標籤爲：-1,1,1,-1,1 ;-1表示該類標籤沒有，1表示該類標籤存在，則這張圖片的標籤編碼爲：人工智能

0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1

2.如何衡量損失？

計算出一張圖片各個標籤的損失，而後取平均值。

3.如何計算精度

計算出一張圖片各個標籤的精度，而後取平均值。

該處理方法的本質：把一個多標籤問題，轉化爲了在每一個標籤上的二分類問題。

損失函數的選擇問題

基於邏輯迴歸的二分類問題

對於logistic迴歸，有：

h_{\theta}(x) = g(\theta^{T}x) = \frac{1}{1+e^{-\theta^{T}x}}

邏輯迴歸有如下優勢：

它的輸入範圍是 $-\infty \to+\infty$ ，而之於恰好爲（0，1），正好知足機率分佈爲（0，1）的要求。咱們用機率去描述分類器，天然比單純的某個閾值要方便不少；
它是一個單調上升的函數，具備良好的連續性，不存在不連續點。

對數損失函數（logarithmic loss function) 或對數似然損失函數(log-likehood loss function) 。

邏輯迴歸中，採用的則是對數損失函數。根據上面的內容，咱們能夠獲得邏輯迴歸的對數似然損失函數cost function：

cost(h_{\theta}(x),y) = \begin{cases} -log(h_{\theta}(x)) & \text {if y=1} \\ -log(1-h_{\theta}(x)) & \text{if y=0} \end{cases}

將以上兩個表達式合併爲一個，則單個樣本的損失函數能夠描述爲：

cost(h_{\theta}(x),y) = -y_ilog(h_{\theta}(x)) - (1-y_i)log(1-h_{\theta}(x))

這就是邏輯迴歸最終的損失函數表達式。

基於 Softmax 的多分類問題

softmax層中的softmax 函數是logistic函數在多分類問題上的推廣，它將一個N維的實數向量壓縮成一個知足特定條件的N維實數向。壓縮後的向量知足兩個條件：

向量中的每一個元素的大小都在[0,1]
向量全部元素的和爲 1

所以，softmax適用於多分類問題中對每個類別的機率判斷，softmax的函數公式以下：

a^L_j = \frac {e^{z^L_j}}{\sum_k e^{z^L_k}}

基於 Softmax 的多分類問題採用的是 log似然代價函數（log-likelihood cost function）來解決。

單個樣本的 log似然代價函數的公式爲：

其中，表示標籤向量的第個份量。由於每每只有一個份量爲 1 其他的份量都爲 0，因此能夠去掉損失函數中的求和符號，化簡爲，

其中，是向量中取值爲 1 對應的第個份量的值。

交叉熵損失函數與 log 似然代價函數關係本質同樣

有的文獻中也稱 log 似然代價函數爲交叉熵損失函數，這兩個都是交叉熵損失函數，可是看起來長的卻有天壤之別。爲何同是交叉熵損失函數，長的卻不同呢？

由於這兩個交叉熵損失函數對應不一樣的最後一層的輸出。第一個對應的最後一層是 sigmoid，用於二分類問題，第二個對應的最後一層是 softmax，用於多分類問題。可是它們的本質是同樣的，請看下面的分析。

首先來看信息論中交叉熵的定義：

交叉熵是用來描述兩個分佈的距離的，神經網絡訓練的目的就是使 g(x) 逼近 p(x)。

sigmoid + 交叉熵

先看看 sigmoid 做爲神經網絡最後一層的狀況。sigmoid 做爲最後一層輸出的話，那就不能吧最後一層的輸出看做成一個分佈了，由於加起來不爲 1。如今應該將最後一層的每一個神經元看做一個分佈，對應的 target 屬於二項分佈(target的值表明是這個類的機率)，那麼第 i 個神經元交叉熵爲

y_i\text{log}(h_{\theta})+(1-y_i)\text{log}(1-h_{\theta})

其實這個式子能夠用求和符號改寫，

其中，

cost(h_{\theta}(x),y) = \begin{cases} -log(a_i) & a_i=h_{\theta} & \text {if } y_i=1 \\ -log(a_i) & a_i=1-h_{\theta} & \text{if } y_i=0 \end{cases}

Softmax + 對數似然

如今來看 softmax 做爲神經網絡最後一層的狀況。g(x)是什麼呢？就是最後一層的輸出 y 。p(x)是什麼呢？就是咱們的one-hot標籤。咱們帶入交叉熵的定義中算一下，就會獲得：

交叉熵損失函數與 log 似然損失函數的總結

注意到不論是交叉熵損失函數與 log 似然損失函數，交叉熵損失函數用於二分類問題， log 似然損失函數用於多分類，可是對於某一個樣本只屬於一個類別，只有一個標籤。若是用 one-hot 編碼樣本的標籤那麼，對於標籤向量只有一個份量的值爲 1 其他的值都爲 0。

因此不論是交叉熵損失函數與 log 似然損失函數，均可以化簡爲，

其中，是向量中取值爲 1 對應的第個份量的值。這兩個長的不同的損失函數其實是對應的不一樣的輸出層。本質上是同樣的。

個人建議是，採用 Kears 中的命名方法，對於二分類的交叉熵損失函數稱之爲 「二分類交叉熵損失函數（binary_crossentropy）」 ，對於多分類的交叉熵損失函數稱之爲 「多類別交叉熵損失函數（categorical_crossentropy）」。

在 Kears 中也有提示（注意: 當使用categorical_crossentropy損失時，你的目標值應該是分類格式 (即，若是你有10個類，每一個樣本的目標值應該是一個10維的向量，這個向量除了表示類別的那個索引爲1，其餘均爲0)。爲了將整數目標值轉換爲分類目標值，你可使用Keras實用函數to_categorical：）

多標籤分類 + 二分類交叉熵損失函數

多標籤問題與二分類問題關係在上文已經討論過了，方法是計算一個樣本各個標籤的損失（輸出層採用sigmoid函數），而後取平均值。把一個多標籤問題，轉化爲了在每一個標籤上的二分類問題。

總結

分類問題名稱	輸出層使用激活函數	對應的損失函數
二分類	sigmoid函數	二分類交叉熵損失函數（binary_crossentropy）
多分類	Softmax函數	多類別交叉熵損失函數（categorical_crossentropy）
多標籤分類	sigmoid函數	二分類交叉熵損失函數（binary_crossentropy）