樹，二叉樹，二叉搜索樹 && 實戰練習

時間 2019-12-28

標籤二叉樹搜索實戰練習欄目應用數學简体版

原文原文鏈接

背景

樹，是一種常見的數據結構，有不少的應用場景，也是面試中的常客。前端

好比：樹的遍歷，分層打印，平攤的數據轉成樹，等等。node

這就須要咱們對樹這種數據結構有個基礎的認識，今天咱們就再回顧一下這種數據結構。面試

正文

今天的內容主要包括：segmentfault

樹
二叉樹
二叉搜索樹
實戰題目

樹

講樹以前，咱們先回顧下鏈表。數據結構

實際上鍊表和樹，圖，都是有一些聯繫的。學習

先看一個單鏈表的示意圖：spa

每一個結點都有個value 和一個next 指向後續結點, 一直向後，串成一個鏈。3d

這種結構很方便，可是也有必定的侷限。指針

好比想一想訪問中間某個結點的時候，或者倒數第幾個結點就只能從頭日後一個一個查，效率不高。code

爲解決這種問題，應運而生的方法有不少，好比雙向鏈表，每一個結點不光有後繼結點，還有前繼結點。

其實再觀察一下，不難發現，若是每一個結點的next有兩個，會是怎麼樣？

就變成了咱們所說的樹。

這是一個普通的二叉樹的結構，每一個結點有兩個next指針，即左右孩子。

二叉樹的一種代碼表示：

這個特殊的鏈表的第一個結點，就是咱們說的樹的根結點。

樹也是分層的，所謂的層，就是距離根結點的距離，如上圖所示。

二叉樹

若是每個結點都有兩個孩子結點，這樣的樹，就是滿二叉樹。

再觀察一下，發現，若是結點還能指回到根結點，或者其餘結點，這個樹會變成什麼樣？

沒錯，就變成了圖。

圖在咱們的生活中也有不少類似的案例，好比你要走到什麼地方，怎麼走最短等等。

簡單總結一下：

鏈表，就是特殊化的樹。
樹，就是特殊化的圖。

二叉搜索樹

二叉搜索樹，是一種特殊的二叉樹。

它能夠是一顆空樹，或者是具備下列性質的二叉樹：

左子樹上全部結點的值，均小於它的根結點的值
右子樹上全部結點的值，均大於它的根結點的值
左右子樹，都是一個合法的二叉搜索樹。

好比：

左孩子上的結點都是小於27的，後孩子上的結點都是大於27的。

這種結構的好處在於，好比咱們要查找一個元素的時候，只須要和根比較。

大於根，就在右子樹，小於就在左子樹，每次搜索，都能減小一半的數據量。

和鏈表相比，查找一個元素，鏈表是O(N), 二叉搜索樹每次都是減一半，就變成了O(log2(N)), 效率得以提高。

最後獻上一個老生常談的比較圖：

二叉搜索樹在最壞的狀況下，會退化成O(N)的，好比，只有右子樹，沒有左子樹，就是一條長長的鏈。

爲了改善這種狀況，後面又發展出了各類各樣的樹，好比下面的

紅黑樹
Splay Tree
AVL Tree

這三種也叫平衡二叉搜索樹，在最壞狀況下，也能保持O(log(n))的時間複雜度

在Java， C++ 的標準庫裏面，二叉搜索樹都是用紅黑樹來實現的。

對紅黑樹有興趣的同窗，能夠看一下維基百科： https://zh.wikipedia.org/wiki...

理論大概就是這麼些，下面咱們就進入到實戰環節。

實戰題目

驗證二叉搜索樹

這是leetcode 的第98題, medium 難度。

給定一個二叉樹，判斷其是不是一個有效的二叉搜索樹。

假設一個二叉搜索樹具備以下特徵：

節點的左子樹只包含小於當前節點的數。
節點的右子樹只包含大於當前節點的數。
全部左子樹和右子樹自身必須也是二叉搜索樹。

示例 1:

輸入:
    2
   / \
  1   3
輸出: true

示例 2:
輸入:
    5
   / \
  1   4
     / \
    3   6

輸出: false

解釋: 
輸入爲: [5,1,4,null,null,3,6]。
根節點的值爲 5 ，可是其右子節點值爲 4 。

我用了三種解法，下面咱們一個一個看。

解法1: 利用升序特性

觀察二叉搜索樹，咱們不難發現，若是是一個合法的二叉搜索數，必定是左結點 < 根結點 < 右結點

這樣獲得的中序遍歷必定是一個升序的，能夠用這種方式來驗證。

簡單回顧下二叉樹的遍歷：

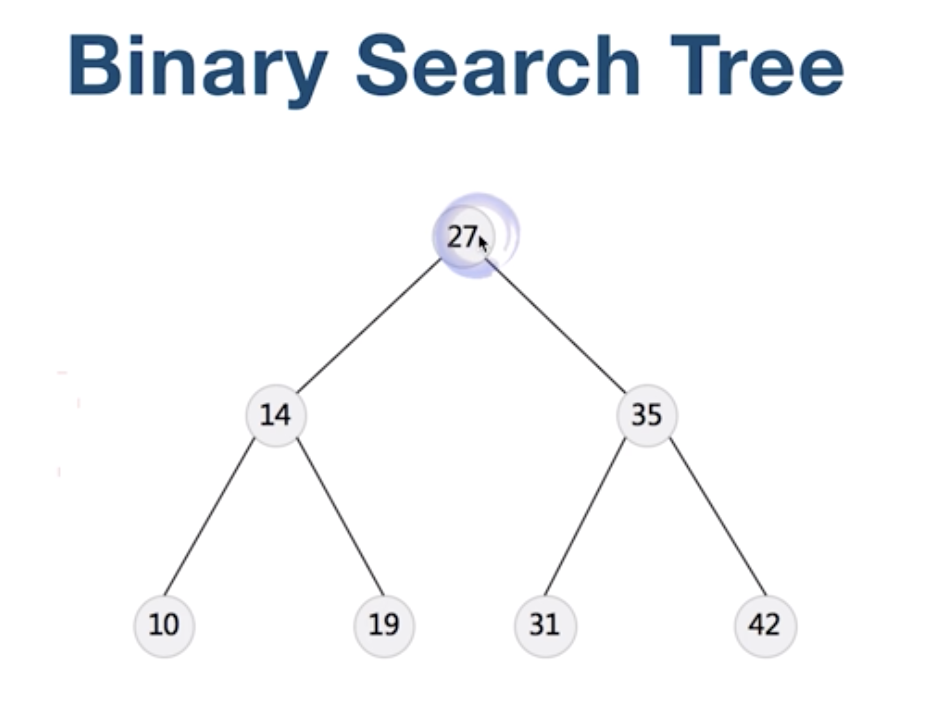
好比這個樹的中序遍歷結果就是： 10 14 19 27 31 35 42

因此利用升序特性，咱們能夠獲得第一種解法：

var isValidBST = function (root) {
    var stack = [];

    // 中序遍歷
    function dfs(root) {
        if (!root) return;
        root.left && dfs(root.left)
        root && stack.push(root.val)
        root.right && dfs(root.right)
    }

    dfs(root)

    for (var i = 0; i < stack.length - 1; i++) {
        if (stack[i] >= stack[i + 1]) return false
    }

    return true;
};

在觀察一下，咱們不難發現， 左結點 < 根結點 < 右結點, 根結點的值必定是夾在左右結點的值中間的，

若是不在這個範圍裏，也必定是不合法的。因此，根據這個思路，能夠獲得解法2.

解法2: 遞歸

var isValidBST = function (root) {

    function isValidBSTHelper(root, min, max) {

        if (root == null) return true; // 空樹也是合法的

        if (root.val <= min || root.val >= max) return false; // 不在範圍內， 不合法
        return isValidBSTHelper(root.left, min, root.val) && isValidBSTHelper(root.right, root.val, max); // 減小一半數據， 繼續往下判斷
    }

    return isValidBSTHelper(root, -Infinity, Infinity)
}

這種解法也很是容易理解。

解法3: 利用特性

第三種解法來自網友，也是利用大小的特性.

即： 任意節點的值必須大於其左子樹的最右節點；同時小於右子樹的最左節點。

從根節點開始檢查，一旦發現不知足則返回false.

代碼實現：

var isValidBST = function (root) {

    function dfs(root) {
        if (root == null) return true

        if (root.left) {
            if (root.left.val >= root.val) return false
            let rightest = getRightest(root.left)
            if (rightest && rightest.val >= root.val) return false

        }
        
        if (root.right) {
            if (root.right.val <= root.val) return false
            let leftest = getLeftest(root.right)
            if (leftest && leftest.val <= root.val) return false
        }

        return dfs(root.left) && dfs(root.right)
    }

    function getRightest(node) {
        while (node && node.right) node = node.right
        return node
    }

    function getLeftest(node) {
        while (node && node.left) node = node.left
        return node
    }

    return dfs(root)
};

代碼稍顯繁瑣，理解一下思路便可。

二叉搜索樹的最近公共祖先

這是leetcode 235題。

給定一個二叉搜索樹, 找到該樹中兩個指定節點的最近公共祖先。

百度百科中最近公共祖先的定義爲：「對於有根樹 T 的兩個結點 p、q，最近公共祖先表示爲一個結點 x.

知足 x 是 p、q 的祖先且 x 的深度儘量大（一個節點也能夠是它本身的祖先

例如，給定以下二叉搜索樹:  root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

輸入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
輸出: 6 
解釋: 節點 2 和節點 8 的最近公共祖先是 6。
示例 2:

輸入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
輸出: 2
解釋: 節點 2 和節點 4 的最近公共祖先是 2, 由於根據定義最近公共祖先節點能夠爲節點自己。
 

說明:

全部節點的值都是惟一的。
p、q 爲不一樣節點且均存在於給定的二叉搜索樹中。

這道題我用了兩種解法。

解法1: 遞歸

遞歸的思路也很是簡單：

若是 p, q 都小於root, 說明解在左子樹。
若是 p, q 都大於root, 說明解在右子樹。
若是一個大於root, 一個小於root, 那root 就是最近的公共祖先。

按照這個思路，實現代碼：

var lowestCommonAncestor = function(root, p, q) {

    // p, q 都小於root, 說明解在左子樹
    if(p.val < root.val && q.val < root.val ) return lowestCommonAncestor(root.left, p, q)

    // p, q 都大於root, 說明解在右子樹
    if(p.val > root.val && q.val > root.val ) return lowestCommonAncestor(root.right, p, q)

    return root
}

解法2: 非遞歸

解法2是解法1的變種，思路都是同樣的，只不過由遞歸改爲了非遞歸。

代碼實現：

var lowestCommonAncestor = function (root, p, q) {
    while (root) {
        if (p.val < root.val && q.val < root.val) {
            root = root.left
        } else if (p.val > root.val && q.val > root.val) {
            root = root.right
        } else {
            return root
        }
    }
}