python數據分析(數據可視化)
數據分析初始階段,一般都要進行可視化處理。數據可視化旨在直觀展現信息的分析結果和構思,令某些抽象數據具象化,這些抽象數據包括數據測量單位的性質或數量。本章用的程序庫matplotlib是創建在Numpy之上的一個Python圖庫,它提供了一個面向對象的API和一個過程式類的MATLAB
API,他們能夠並行使用。本文涉及的主題有:python
- matplotlib簡單繪圖
- 對數圖
- 散點圖
- 圖例和註解
- 三維圖
- pandas繪圖
- 時滯圖
- 自相關圖
- Plot.ly
一、matplotlib繪圖入門
代碼:api
import matplotlib.pyplot as plt
import numpy as np
x=np.linspace(0,20) #linspace()函數指定橫座標範圍
plt.plot(x,.5+x)
plt.plot(x,1+2*x,'--')
plt.show()
[/code]
運行結果:
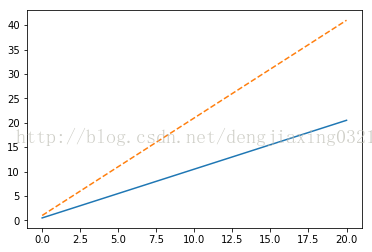
![]()
經過show函數將圖形顯示在屏幕上,也能夠用savefig()函數把圖形保存到文件中。
## 二、對數圖
所謂對數圖,實際上就是使用對數座標繪製的圖形。對於對數刻度來講,其間隔表示的是變量的值在數量級上的變化,這與線性刻度有很大的不一樣。對數圖又分爲兩種不一樣的類型,其中一種稱爲雙對數圖,它的特色是兩個座標軸都採用對數刻度,對應的matplotlibh函數是matplotlib.pyplot..loglog()。半對數圖的一個座標軸採用線性刻度,另外一個座標軸使用對數刻度,它對應的matplotlib
API是semilogx()函數和semilogy()函數,在雙對數圖上,冪律表現爲直線;在半對數圖上,直線則表明的是指數律。
摩爾定律大意爲集成電路上晶體管的數量每兩年增長一倍。在https://en.wikipedia.org/wiki/Transistor_count#Microprocessors頁面有一個數據表,記錄了不一樣年份微處理器上晶體管的數量。咱們爲這些數據製做一個CSV文件,名爲transcount.csv,其中只包含晶體管數量和年份值。
代碼:
```code
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
df=pd.read_csv('H:\Python\data\\transcount.csv')
df=df.groupby('year').aggregate(np.mean) #按年份分組,以數量均值聚合
#print grouped.mean()
years=df.index.values #獲得全部年份信息
counts=df['trans_count'].values
#print counts
poly=np.polyfit(years,np.log(counts),deg=1) #線性擬合數據
print "poly:",poly
plt.semilogy(years,counts,'o')
plt.semilogy(years,np.exp(np.polyval(poly,years))) #polyval用於對多項式進行評估
plt.show()
#print df
#df=df.groupby('year').aggregate(np.mean)
[/code]
運行結果:
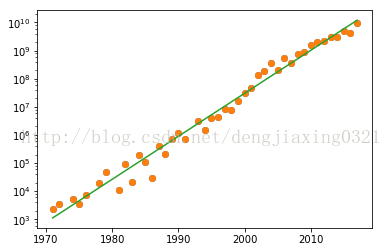
![]()
實線表示的是趨勢線,實心圓表示的是數據點。
## 三、散點圖
散點圖能夠形象展現直角座標系中兩個變量之間的關係,每一個數據點的位置實際上就是兩個變量的值。泡式圖是對散點圖的一種擴展。在泡式圖中,每一個數據點都被一個氣泡所包圍,它由此得名;而第三個變量的值正好能夠用來肯定氣泡的相對大小。
在https://en.wikipedia.org/wiki/Transistor_count#GPU頁面上,有個記錄GPU晶體數量的數據表,咱們用這些晶體管數量年份數據新建表gpu_transcount.csv。藉助matplotlib
API提供的scatter()函數繪製散點圖。
代碼:
```code
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
df=pd.read_csv('H:\Python\data\\transcount.csv')
df=df.groupby('year').aggregate(np.mean)
gpu=pd.read_csv('H:\Python\data\\gpu_transcount.csv')
gpu=gpu.groupby('year').aggregate(np.mean)
df=pd.merge(df,gpu,how='outer',left_index=True,right_index=True)
df=df.replace(np.nan,0)
print df
years=df.index.values
counts=df['trans_count'].values
gpu_counts=df['gpu_counts'].values
cnt_log=np.log(counts)
plt.scatter(years,cnt_log,c=200*years,s=20+200*gpu_counts/gpu_counts.max(),alpha=0.5) #表示顏色,s表示標量或數組
plt.show()
[/code]
運行結果
```code
trans_count gpu_counts
year
1971 2300 0.000000e+00
1972 3500 0.000000e+00
1974 5400 0.000000e+00
1975 3510 0.000000e+00
1976 7500 0.000000e+00
1978 19000 0.000000e+00
1979 48500 0.000000e+00
1981 11500 0.000000e+00
1982 94500 0.000000e+00
1983 22000 0.000000e+00
1984 190000 0.000000e+00
1985 105333 0.000000e+00
1986 30000 0.000000e+00
1987 413000 0.000000e+00
1988 215000 0.000000e+00
1989 745117 0.000000e+00
1990 1200000 0.000000e+00
1991 692500 0.000000e+00
1993 3100000 0.000000e+00
1994 1539488 0.000000e+00
1995 4000000 0.000000e+00
1996 4300000 0.000000e+00
1997 8150000 3.500000e+06
1998 7500000 0.000000e+00
1999 16062200 1.533333e+07
2000 31500000 2.500000e+07
2001 45000000 5.850000e+07
2002 137500000 8.500000e+07
2003 190066666 1.260000e+08
2004 352000000 1.910000e+08
2005 198500000 3.120000e+08
2006 555600000 5.325000e+08
2007 371600000 4.882500e+08
2008 733200000 7.166000e+08
2009 904000000 9.155000e+08
2010 1511666666 1.804143e+09
2011 2010000000 1.370952e+09
2012 2160625000 3.121667e+09
2013 3015000000 3.140000e+09
2014 3145000000 3.752500e+09
2015 4948000000 8.450000e+09
2016 4175000000 7.933333e+09
2017 9637500000 8.190000e+09
[/code]
![]()
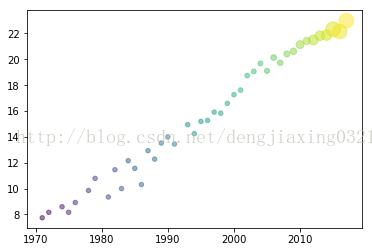
## 四、圖例和註解
要想作出讓人眼前一亮的神圖,圖例和註解確定是少不了的。通常狀況下,數據圖都帶有下列輔助信息。
* 用來描述圖中各數據序列的圖例,matplotlib提供的legend()函數能夠爲每一個數據序列提供相應的標籤。
* 對圖中要點的註解。能夠藉助matplotlib提供的annotate()函數。
* 橫軸和縱軸的標籤,能夠經過xlabel()和ylabel()繪製出來。
* 一個說明性質的標題,一般由matplotlib的title函數來提供.
* 網格,對於輕鬆定位數據點很是有幫助。grid()函數能夠用來決定是否使用網格。
代碼:
```code
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
df=pd.read_csv('H:\Python\data\\transcount.csv')
df=df.groupby('year').aggregate(np.mean)
gpu=pd.read_csv('H:\Python\data\\gpu_transcount.csv')
gpu=gpu.groupby('year').aggregate(np.mean)
df=pd.merge(df,gpu,how='outer',left_index=True,right_index=True)
df=df.replace(np.nan,0)
years=df.index.values
counts=df['trans_count'].values
gpu_counts=df['gpu_counts'].values
#print df
poly=np.polyfit(years,np.log(counts),deg=1)
plt.plot(years,np.polyval(poly,years),label='Fit')
gpu_start=gpu.index.values.min()
y_ann=np.log(df.at[gpu_start,'trans_count'])
ann_str="First GPU\n %d"%gpu_start
plt.annotate(ann_str,xy=(gpu_start,y_ann),arrowprops=dict(arrowstyle="->"),xytext=(-30,+70),textcoords='offset points')
cnt_log=np.log(counts)
plt.scatter(years,cnt_log,c=200*years,s=20+200*gpu_counts/gpu_counts.max(),alpha=0.5,label="Scatter") #表示顏色,s表示標量或數組
plt.legend(loc="upper left")
plt.grid()
plt.xlabel("Year")
plt.ylabel("Log Transistor Counts",fontsize=16)
plt.title("Moore's Law & Transistor Counts")
plt.show()
運行結果:數組
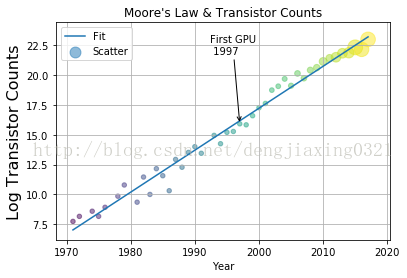ide
五、三維圖
Axes3D是由matplotlib提供的一個類,能夠用來繪製三維圖。經過講解這個類的工做機制,就可以明白麪向對象的matplotlib
API的原理了,matplotlib的Figure類是存放各類圖像元素的頂級容器。函數
代碼:工具
from mpl_toolkits.mplot3d.axes3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
df=pd.read_csv('H:\Python\data\\transcount.csv')
df=df.groupby('year').aggregate(np.mean)
gpu=pd.read_csv('H:\Python\data\\gpu_transcount.csv')
gpu=gpu.groupby('year').aggregate(np.mean)
df=pd.merge(df,gpu,how='outer',left_index=True,right_index=True)
df=df.replace(np.nan,0)
fig=plt.figure()
ax=Axes3D(fig)
X=df.index.values
Y=np.log(df['trans_count'].values)
X,Y=np.meshgrid(X,Y)
Z=np.log(df['gpu_counts'].values)
ax.plot_surface(X,Y,Z)
ax.set_xlabel('Year')
ax.set_ylabel('Log CPU transistor counts')
ax.set_zlabel('Log GPU transistor counts')
ax.set_title('Moore Law & Transistor counts')
plt.show()
[/code]
運行結果:
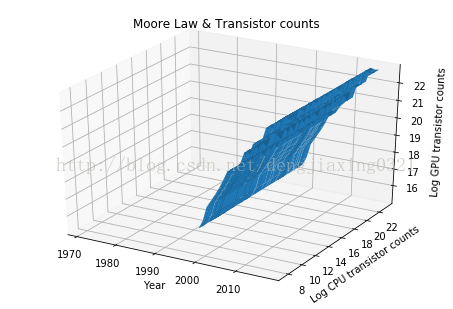
## 六、pandas繪圖
pandas的Series類和DataFrame類中的plot()方法都封裝了相關的matplotlib函數。若是不帶任何參數,使用plot方法繪製圖像以下:
代碼:
```code
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
df=pd.read_csv('H:\Python\data\\transcount.csv')
df=df.groupby('year').aggregate(np.mean)
gpu=pd.read_csv('H:\Python\data\\gpu_transcount.csv')
gpu=gpu.groupby('year').aggregate(np.mean)
df=pd.merge(df,gpu,how='outer',left_index=True,right_index=True)
df=df.replace(np.nan,0)
df.plot()
df.plot(logy=True) #建立半對數圖
df[df['gpu_counts']>0].plot(kind='scatter',x='trans_count',y='gpu_counts',loglog=True) #loglog=True 生成雙對數
plt.show()
運行結果:網站
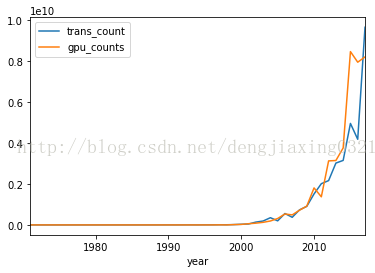url
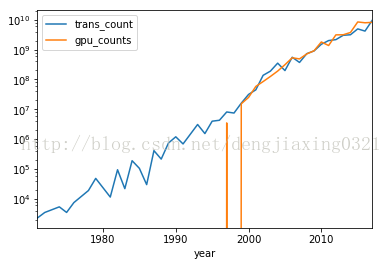spa
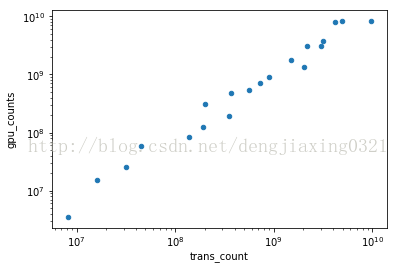.net
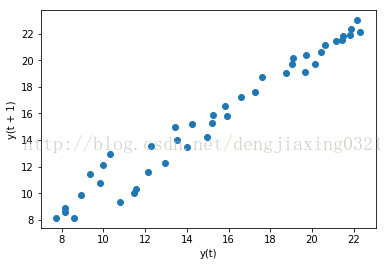
七、時滯圖
時滯圖實際上就是一個散點圖,只不過把時間序列的圖像及相同序列在時間軸上後延圖像放一塊兒展現而已。例如,咱們能夠利用這種圖考察今年的CPU晶體管數量與上一年度CPU晶體管數量之間的相關性。能夠利用pandas字庫pandas.tools.plotting中的lag_plot()函數來繪製時滯圖,滯默認爲1。
代碼:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from pandas.tools.plotting import lag_plot
df=pd.read_csv('H:\Python\data\\transcount.csv')
df=df.groupby('year').aggregate(np.mean)
gpu=pd.read_csv('H:\Python\data\\gpu_transcount.csv')
gpu=gpu.groupby('year').aggregate(np.mean)
df=pd.merge(df,gpu,how='outer',left_index=True,right_index=True)
df=df.replace(np.nan,0)
lag_plot(np.log(df['trans_count']))
plt.show()
[/code]
運行結果:
## 八、自相關圖
自相關圖描述的是時間序列在不一樣時間延遲狀況下的自相關性。所謂自相關,就是一個時間序列與相同數據在不一樣時間延遲狀況下的相互關係。利用pandas子庫pandas.tools.plotting
中的autocorrelation_plot()函數,就能夠畫出自相關圖了。
代碼:
```code
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from pandas.tools.plotting import autocorrelation_plot
df=pd.read_csv('H:\Python\data\\transcount.csv')
df=df.groupby('year').aggregate(np.mean)
gpu=pd.read_csv('H:\Python\data\\gpu_transcount.csv')
gpu=gpu.groupby('year').aggregate(np.mean)
df=pd.merge(df,gpu,how='outer',left_index=True,right_index=True)
df=df.replace(np.nan,0)
autocorrelation_plot(np.log(df['trans_count'])) #繪製自相關圖
plt.show()
[/code]
運行結果:
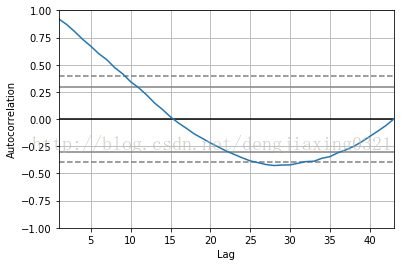
從圖中能夠看出,較之於時間上越遠(即時間延遲越大)的數值,當前的數值與時間上越接近(及時間延遲越小)的數值相關性越大;當時間延遲極大時,相關性爲0;
## 九、Plot.ly
Plot.ly其實是一個網站,它不只提供了許多數據可視化的在線工具,同時還提供了可在用戶機器上使用的對應的python庫。能夠經過Web接口或以本地導入並分析數據,能夠將分析結果公佈到Plot.ly網站上。
安裝plotly庫:pip install plotly
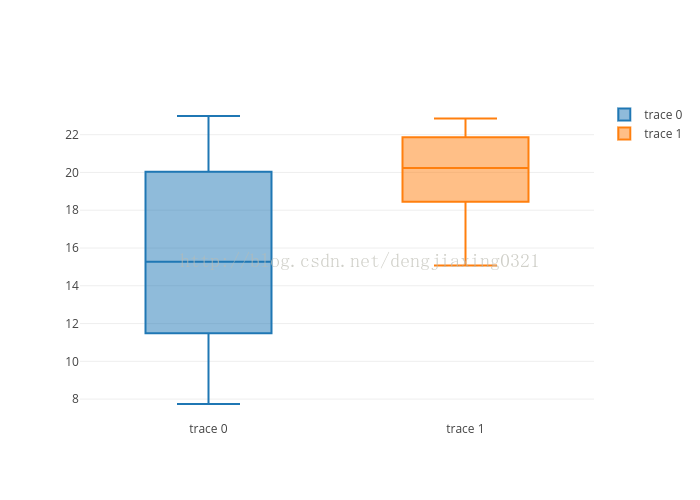
先在plotly註冊一個帳號,而後產生一個api_key。最後能夠繪製箱形圖。
代碼:
```code
import numpy as np
import pandas as pd
import plotly.plotly as py
from plotly.graph_objs import *
from getpass import getpass
df=pd.read_csv('H:\Python\data\\transcount.csv')
df=df.groupby('year').aggregate(np.mean)
gpu=pd.read_csv('H:\Python\data\\gpu_transcount.csv')
gpu=gpu.groupby('year').aggregate(np.mean)
df=pd.merge(df,gpu,how='outer',left_index=True,right_index=True)
df=df.replace(np.nan,0)
api_key=getpass()
py.sign_in(username='dengjiaxing',api_key='qPCrc5EA7unk9PlhNwLG')
counts=np.log(df['trans_count'].values)
gpu_counts=np.log(df['gpu_counts'].values)
data=Data([Box(y=counts),Box(y=gpu_counts)])
plot_url=py.plot(data,filename='moore-law-scatter')
print plot_url
[/code]
運行結果:
- 1. python數據分析(數據可視化)
- 2. 數據分析之數據可視化
- 3. 數據分析——數據可視化
- 4. Python 數據分析可視化
- 5. python數據可視化分析庫matplotlib
- 6. Python: 數據分析與可視化matplotlib
- 7. python數據可視化seaborn(四)—— 分類數據可視化
- 8. Python數據可視化——分佈數據可視化
- 9. python數據可視化seaborn(二)—— 分佈數據可視化
- 10. Python數據分析實戰(3)Python實現數據可視化
- 更多相關文章...
- • SQLite 分離數據庫 - SQLite教程
- • R 數據框 - R 語言教程
- • Flink 數據傳輸及反壓詳解
- • TiDB 在摩拜單車在線數據業務的應用和實踐
-
每一个你不满意的现在,都有一个你没有努力的曾经。