分享 HT 實用技巧：實現指南針和 3D 魔方導航

前言

三維場景時常須要一個導航標識，用來肯定場景所處的方位。

通常有兩種表現形式：指南針、小方盒(方位魔方)。

參考一下百度百科中的 maya 界面，能夠看到右上角有一個標識方位的小盒子，說的就是它：

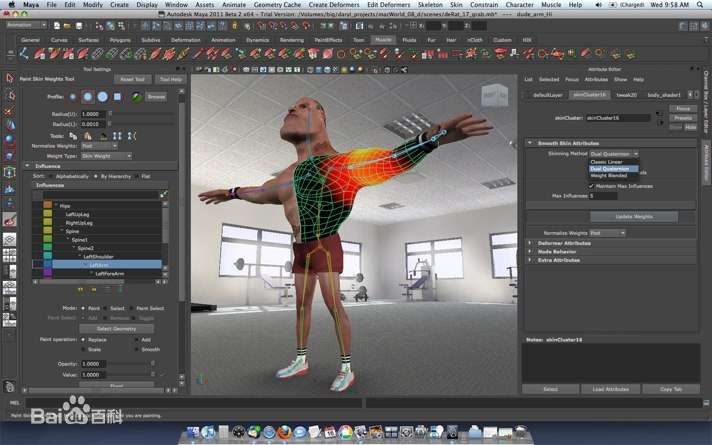
Hightopo 的 HT for Web 產品能夠很方便地構造輕量化的 3D 可視化場景，在 web 端 咱們能夠利用 HT 2D 引擎 和 3D 渲染引擎 來實現這個功能，搭建一個簡易的類 maya 操做界面。

預覽地址： https://www.hightopo.com/demo/compass-and-directionbox/

界面簡介及效果預覽

在這個界面裏面咱們用到了一個二維場景和兩個三維場景，具體效果以下：

功能實現

先來描述一下頁面佈局：

指南針 經過在 ht.graph.GraphView 中給一個圖元設置一個事先繪製好的圖標來實現，只需把它放在圖紙的左上角（即下圖中的位置 1）便可。

方位魔方 經過在一個小場景 （ht.graph3d.Graph3dView）中放置一個魔方 obj 模型來實現，而後把這個小場景放置在圖紙的右上角（即下圖中的位置 2） 便可。

主三維場景（ht.graph3d.Graph3dView）做爲背景放置在整個二維頁面的下方（即下圖中的位置 3）。

代碼示例：

const g3d = new ht.graph3d.Graph3dView();
g3d.setOriginAxisVisible(true);
g3d.setGridVisible(true);
g3d.addToDOM();
const g2d = new ht.graph.GraphView();
g2d.deserialize('displays/test.json', json => {
    g2d.addToDOM(g3d.getView());
});

位置關係：

指南針同步

先約定一下方位，咱們將 Z 軸的負半軸的方向做爲北方，Z 軸正半軸做爲南方，X 軸的正半軸做爲東方，X 軸的負半軸做爲西方。

因爲 指南針 的目的是用於指示鳥瞰圖中的方位，因此與 Y 軸並無什麼關係，咱們能夠將整個計算過程放在二維空間中進行。

代碼示例：

const eye = this.g3d.getEye();
const center = this.g3d.getCenter();
const v = new ht.Math.Vector2(eye[0], eye[2]);
const v2 = new ht.Math.Vector2(center[0], center[2]);
const angle = v.sub(v2).angle() - Math.PI / 2;
compass.setRotation(-angle);
compass.a('angle', angle);
compass.a('angle2', angle);

在這段代碼中，咱們用 eye （相機） 和 center （觀測點）來構建兩個二維向量 （ht.Math.Vector2），捨棄掉 Y 軸上的份量。

利用向量減法，求得由 center 指向 eye 的向量並存入變量 v 中，利用 angle() 方法能夠獲取到當前向量與 x 正半軸 （即正東方向）的夾角（弧度制），爲何要減去 Math.PI / 2 呢，由於咱們計算求得的是與 x 軸的夾角，而指南針的正方向（北方）是對應着 z 軸的負半軸。

求得了旋轉角度後，經過 setRotation() 方法咱們能夠設置 指南針 圖元的旋轉角度，爲何要取一個負值（- angle）？由於當視線逆時針轉動的時候，座標軸 和 指南針 相對於人眼是沿反方向運動的，也就是順時針旋轉。

利用 HT 2D 引擎提供的 數據綁定 的功能，輪盤圖標 和 角度圖標 的旋轉角度能夠經過給 compass 這個節點設置屬性值來實時動態改變。

每一次視線發生改變都須要進行如上的計算和設置，咱們能夠經過給三維場景組件增長一個屬性監聽器來實現：

graph3dView.addPropertyChangeListener(e=>{
    if(e.property === 'eye' || e.property === 'center'){
        changeCompass();
        //...
    }
});

圖例參考：

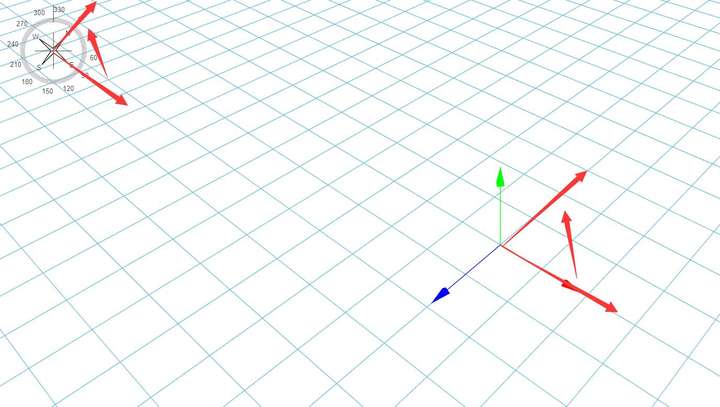
方位魔方同步

先約定一下方位，X 正半軸爲右，負半軸爲左； Y 正半軸爲頂，負半軸爲底；Z 正半軸爲前，負半軸爲後。

方位魔方不一樣於指南針，它用於呈現三維空間中的視線方位。

與此同時，它也是一個能夠交互的方位操縱桿，能夠方便快捷的將當前視角變爲頂視圖、側視圖等。

視線改變觸發魔方變換

代碼示例：

graph3dView.addPropertyChangeListener(e => {
    if (e.property === 'eye') {
        const newValue = e.newValue;
        const vEye = new ht.Math.Vector3(newValue[0], newValue[1], newValue[2]).normalize();
        graph3dView2.setEye([300 * vEye.x, 300 * vEye.y, 300 * vEye.z]);
    }
});

在上述代碼中咱們經過監聽主三維場景（graph3dView） 中 eye 屬性的變化來動態改變小場景（graph3dView2） 中的 eye 的位置， 來達到聯動的效果。

其中，e.newValue 會獲取到場景視點改變後的值，咱們用這個值構建一個三維向量（ht.Math.Vector3）並調用 normalize() 方法進行歸一化，這樣可使得任何角度、位置求得的距離都保持一致。

將求得的份量乘以 300 的緣由在於這個距離觀測小方塊不大不小剛合適，固然也能夠根據須要改爲別的值。

效果示例：

點擊魔方改變場景視角

要想實現點擊魔方來改變主場景中的視線，須要一個很是關鍵的信息，那就是鼠標究竟點擊了小魔方的哪個面。

在這裏咱們須要用到一個求交點的方法： graph3dView.intersectObject(event, data)，該方法會返回一個對象，該對象用於描述點擊的位置信息， 其中 world 屬性用來表示點擊位置的世界座標。

代碼示例：

graph3dView2.addInteractorListener(event => {
    if (event.kind === 'clickData') {
        const obj = graph3dView2.intersectObject(event.event, event.data);
        if(obj) {
            const world = obj.world;
            //...
        }
    }
});

拿到了這個描述點擊位置的 world 屬性咱們就能夠比較輕鬆地算出點擊了哪一個面，由於咱們的小方塊是放置在原點處，而且它是規則的六面體，這兩個關鍵信息決定了不管點擊它的哪個面，所點擊的那個面它所對應的軸的份量的值必定會大於它在另外兩個軸的份量，所以咱們能夠簡單的判斷三份量中哪一個值較大就能肯定視線更靠近哪一個軸，而後經過判斷份量的正負號來判斷是在正半軸仍是負半軸。

判斷了出了點擊的哪一個面以後，只須要在兩個三維場景中分別設置各自視點（eye） 的位置便可。

代碼示例：

const world = obj.world;
const x = world.x;
const y = world.y;
const z = world.z;
if (Math.abs(x) - Math.abs(y) > 0 && Math.abs(x) - Math.abs(z) > 0) {
    if (x > 0) {
        graph3dView2.setEye([300, 0, 0]);
        graph3dView.setEye([this._distance, 0, 0]);
        graph3dView2.setCenter([0, 0, 0]);
        this._g3d.setCenter([0, 0, 0]);
    } else {
        graph3dView2.setEye([-300, 0, 0]);
        graph3dView.setEye([-this._distance, 0, 0]);
        graph3dView2.setCenter([0, 0, 0]);
        graph3dView.setCenter([0, 0, 0]);
    }
} else if (Math.abs(y) - Math.abs(x) > 0 && Math.abs(y) - Math.abs(z) > 0) {
    //...
}

其中，this._distance 是用來描述主場景中視線與原點的距離，可根據須要來調整，300 與以前的描述一致，是小場景中一個比較合適的視角位置，也能夠根據須要調整。

最後咱們還須要處理一下小方塊點擊變色的問題（這也不見得是個問題，視需求而定），能夠在點擊事件監聽器的最後作以下設置：

1 const sm = graph3dView2.dm().getSelectionModel();
2 sm.setSelection(null);

點擊魔方各個面效果演示：

總結

直觀的方位指示在室內定位、GIS、車站、機場等諸多場景中有着普遍的應用，利用 HT 提供的二三維引擎能夠輕鬆地實現。

web 3D 有無限的想象空間，有着很是豐富的數據呈現方式，更有着諸多讓人眼前一亮的可視化效果，等着咱們去將這些數據呈現方式在各個行業中落地，HT 在這方面作了大量的探索和嘗試，例如這個好玩兒的太陽系監控系統：https://www.hightopo.com/demo/solar-system/

2019 咱們也更新了數百個工業互聯網 2D/3D 可視化案例集，在這裏你能發現許多新奇的實例，也能發掘出不同的工業互聯網：《分享數百個 HT 工業互聯網 2D 3D 可視化應用案例之 2019 篇》，更多行業應用實例能夠參考官網案例連接：

https://www.hightopo.com/demo...