深度學習基礎--感知器
深度學習基礎--感知器
本文將介紹感知機這一算法。感知機是由美國學者Frank Rosenblattt 在1957年提出來的。爲什麼咱們如今還要學習之前的算法?由於感知機是做爲神經網絡起源的算法。前端
嚴格的說,本文所說的感知機應該稱爲「人工神經元」或「樸素感知機」,可是不少基本的處理都是共通的,因此這裏簡單的稱爲「感知機」。
本章咱們將簡單介紹一下感知機,並應用感知機解決一些簡單的問題,但願讀者經過這個過程熟悉感知機。
2.1 感知機是什麼
感知機接受多個輸入信號,輸出一個信號。這裏所說的信號能夠想象成電流那樣具有流動的東西。像電流流過導線,向前方輸送電子同樣,感知機的信號也會造成流,向前方輸送信息。可是,和實際的電流不一樣的是,感知機信號只有"流/和不流"兩種取值。分別是,0對應"不流",即不傳遞信號,1對應"流",即傳遞信號。算法
圖2-1是一個接受兩個輸入信號的感知機的例子。$x_1$、$x_2$是輸入信號,$y$是輸出信號,$w_1$、$w_2$是權重。圖中的圓圈(O)稱爲「神經元」或者「節點」。
輸入信號被送往神經元時,會被乘以固定的權重($w_1x_1$)。神經元會計算傳送過來的信號的總和,只有當這個總和超過了某個閾值 $\theta$,纔會輸出1。這也被稱爲「神經元被激活」。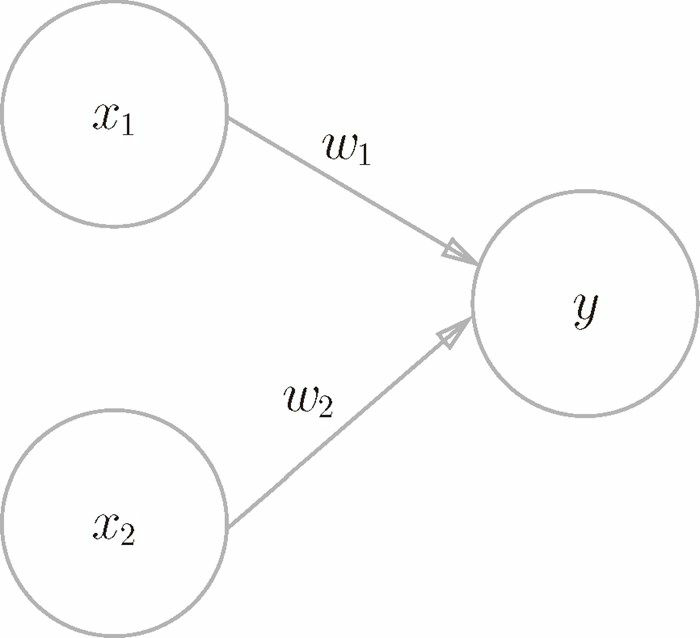 網絡
網絡
感知機的運行原理用數學表達式表示以下
$$y = \left\{ {\begin{array}{*{20}{c}} 0&{(w_1x_1+w_2x_2 \le \theta )} \\1&{(w_1x_1+w_2x_2 > \theta )} \end{array}} \right.$$機器學習
感知機的每一個輸入信號都有各自固有的權重,這些權重發揮着控制各個信號的重要性的做用。也就是說,權重越大,對應該權重的信號的重要性就越高。學習
權重至關於電流裏所說的電阻。電阻是決定電流流動難度的參數,電阻越低,經過的電流就越大。而感知機的權重則是值越大,經過的信號就越大。不論是電阻仍是權重,在控制信號流動難度(或者流動容易度)這一點上的做用都是同樣的。
2.2 邏輯電路
2.2.1 與門
如今讓咱們考慮用感知機來解決簡單的問題。這裏首先以邏輯電路爲題材來思考一下與門。
與門是有兩個輸入和一個輸出的門電路。圖 2-2 這種輸入信號和輸出信號的對應表稱爲「真值表」。如圖 2-2 所示,與門僅在兩個輸入均爲1的時候輸出纔是1,其餘時候則輸出爲0spa
| $x_1$ | $x_2$ | $y$ |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
下面考慮用感知機來表示這個與門。須要作的就是肯定能知足圖 2-2 的真值表的$w_1$、$w_2$、$\theta$ 的值。
那麼,設定什麼樣的值才能製做出知足圖 2-2 的條件的感知機呢?
實際上,知足圖 2-2 的條件的參數的選擇方法有無數多個。好比,當
($w_1$,$w_2$,$\theta$)=(0.5,0.5,0.7)時,能夠知足圖2-2的條件。
($w_1$,$w_2$,$\theta$)=(0.5,0.5,0.8) 或者($w_1$,$w_2$,$\theta$)=(1.0,1.0,1.0)也知足與門條件。設定這樣的參數後,當$x_1$和$x_2$同時爲1的時候,信號的加權總和纔會超過給定的$\theta$。blog
2.2.2 與非門和或門
接着,咱們再來考慮一下與非門(NAND gate)。NAND 是 Not AND 的意思,與非門就是顛倒了與門的輸出。用真值表表示的話,如圖 2-3 所示,僅當$x_1$和$x_2$同時爲 1 時輸出 0,其餘時候則輸出 1。那麼與非門的參數又能夠是什麼樣的組合呢?ip
| $x_1$ | $x_2$ | $y$ |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
要表示與非門,能夠用($w_1$,$w_2$,$\theta$)=(-0.5,-0.5,-0.7)這樣的組合(其餘的組合也是無限存在的)。實際上,只要把實現與門的參數值的符號取反,就能夠實現與非門。深度學習
接下來看一下圖 2-4 所示的或門。或門是「只要有一個輸入信號是 1,輸出就爲 1」的邏輯電路。那麼咱們來思考一下,應該爲這個或門設定什麼樣的參數呢?數學
| $x_1$ | $x_2$ | $y$ |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
這裏決定感知機參數的並非計算機,而是咱們人。咱們看着真值表這種「訓練數據」,人工考慮(想到)了參數的值。而機器學習的問題就是將這個決定參數值的工做交由計算機自動進行。學習 是肯定合適的參數的過程,而人要作的是思考感知機的構造(模型),並把訓練數據交給計算機。
如上所示,咱們已經知道使用感知機能夠表示與門、與非門、或門的邏輯電路。這裏重要的一點是:與門、與非門、或門的感知機構造是同樣的。實際上,3個門電路只有參數的值(權重和閾值)不一樣。也就是說,相同構造的感知機(模型),只需經過適當地調整參數的值,就能夠像「變色龍演員」表演不一樣的角色同樣,變身爲與門、與非門、或門。
2.3 感知機的侷限性
到這裏咱們已經知道,使用感知機能夠實現與門、與非門、或門三種邏輯電路。如今咱們來考慮一下異或門(XOR gate)
2.3.1 異或門
異或門也被稱爲邏輯異或 電路。如圖 2-5 所示,僅當$x_1$或$x_1$中的一方爲 1 時,纔會輸出 1(「異或」是拒絕其餘的意思)。那麼,要用感知機實現這個異或門的話,應該設定什麼樣的權重參數呢?
| $x_1$ | $x_2$ | $y$ |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
實際上,用前面介紹的感知機是沒法實現這個異或門的。爲何用感知機能夠實現與門、或門,卻沒法實現異或門呢?下面咱們嘗試經過畫圖來思考其中的緣由。
咱們將感知機形式修改成另一種實現形式。在此以前,首先把式(2.1)的 θ 換成 -b ,因而就能夠用式(2.2)來表示感知機的行爲。
$$y = \left\{ {\begin{array}{*{20}{c}} 0&{(b+w_1x_1+w_2x_2 \le 0)}\\ 1&{(b+w_1x_1+w_2x_2 > 0 )} \end{array}} \right.$$
雖然有一個符號不一樣,但表達的內容是徹底相同的。此處,$b$ 稱爲偏置 $w_1$和$w_2$稱爲權重 。
首先,咱們試着將或門的動做形象化。或門的狀況下,當權重參數爲$(b,$w_1$,$w_2$)=(-0.5,1.0,1.0)$時,可知足圖2-4的真值表條件。此時,感知機可用以下表達式表示
$$y = \left\{ {\begin{array}{*{20}{c}} 0&{(-0.5+x_1+x_2 \le 0)} \\1&{(-0.5+x_1+x_2 > 0 )} \end{array}} \right.$$
上式表示的感知機會由直線$-0.5+x_1+x_2=0$分割的兩個空間。其中一個空間輸出1,另一個空間輸出0,如圖2-6所示。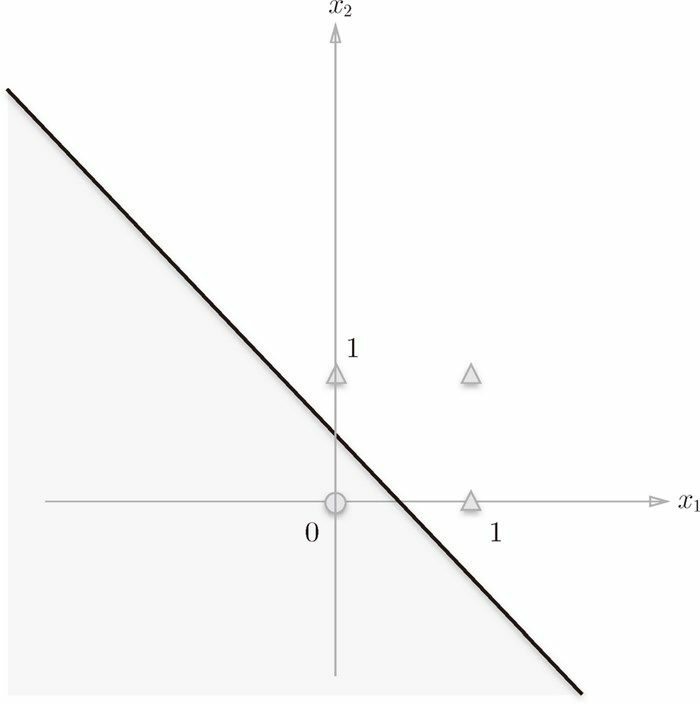
或門在$(x_1,x_2)=(0,0)$時輸出 0,在$(x_1,x_2)$爲 (0, 1)、(1, 0)、(1, 1) 時輸出 1。圖 2-6 中○ 表示 0,▲表示 1。若是想製做或門,須要用直線將圖 2-6 中的○和△分開。實際上,剛纔的那條直線就將這 4 個點正確地分開。
那麼,換成異或門的話會如何呢?可否像或門那樣,用一條直線做出分割圖 2-7 中的○和△的空間呢?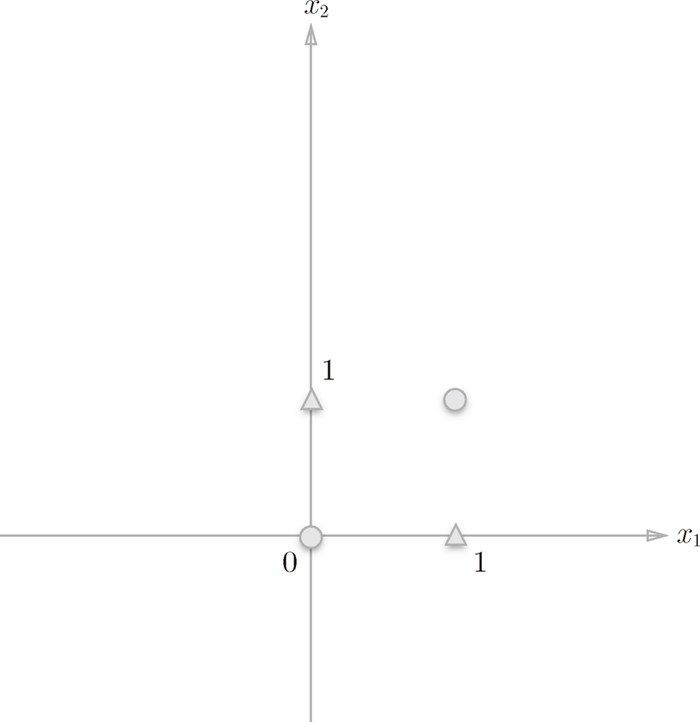
想要用一條直線將圖 2-7 中的○和△分開,不管如何都作不到。事實上,用一條直線是沒法將○和△分開的。
2.3.2 線性與非線性
圖 2-7 中的○和△沒法用一條直線分開,可是若是將「直線」這個限制條件去掉,就能夠實現了。好比,咱們能夠像圖 2-8 那樣,做出分開○和△的空間。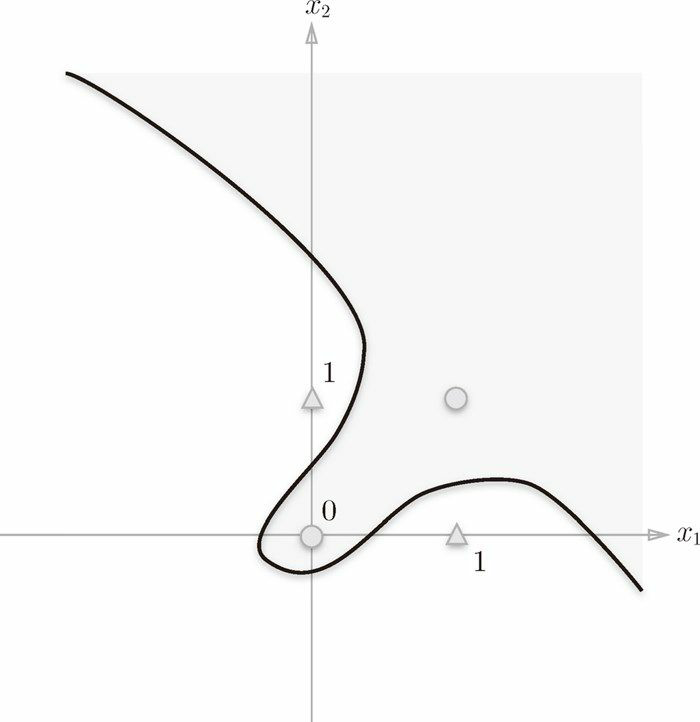
感知機的侷限性就在於它只能表示由一條直線分割的空間。圖 2-8 這樣彎曲的曲線沒法用感知機表示。另外,由圖 2-8 這樣的曲線分割而成的空間稱爲非線性 空間,由直線分割而成的空間稱爲線性 空間。線性、非線性這兩個術語在機器學習領域很常見,能夠將其想象成圖 2-6 和圖 2-8 所示的直線和曲線。
2.4 多層感知機
感知機不能表示異或門讓人深感遺憾,但也無需悲觀。實際上,感知機的絕妙之處在於它能夠「疊加層」(經過疊加層來表示異或門是本節的要點)。這裏,咱們暫且不考慮疊加層具體是指什麼,先從其餘視角來思考一下異或門的問題。
2.4.1 門電路的組合
異或門的製做方法有不少,其中之一就是組合咱們前面作好的與門、與非門、或門進行配置。這裏,與門、與非門、或門用圖 2-9 中的符號表示。另外,圖 2-9中與非門前端的○表示反轉輸出的意思:
那麼,請思考一下,要實現異或門的話,須要如何配置與門、與非門和或門呢?這裏給你們一個提示,用與門、與非門、或門代替圖 2-10 中的各個「?」,就能夠實現異或門。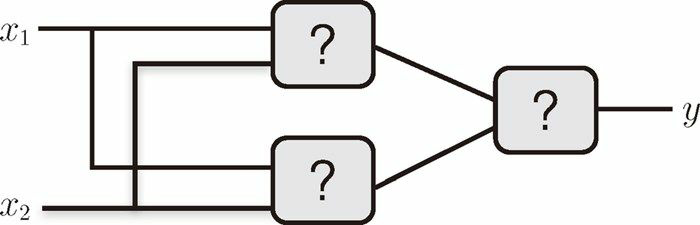
2.3 節講到的感知機的侷限性,嚴格地講,應該是「單層感知機沒法表示異或門」或者「單層感知機沒法分離非線性空間」。接下來,咱們將看到經過組合感知機(疊加層)就能夠實現異或門。
異或門能夠經過圖 2-11 所示的配置來實現。這裏,$x_1$ 和 $x_2$ 表示輸入信號,$y$ 表示輸出信號。 和 是與非門和或門的輸入,而與非門和或門的輸出($s_1$、$s_2$)則是與門的輸入。
如今,咱們來確認一下圖 2-11的配置是否真正實現了異或門。這裏,把$s_1$做爲與非門的輸出,把$s_2$ 做爲或門的輸出,填入真值表中。結果如圖2-12所示,觀察$x_1$、$x_2$、$y$,能夠發現確實符合異或門的輸出。
| ($x_1$、$x_2$) | ($s_1$、$s_2$) | $y$ |
|---|---|---|
| (0,0) | (1,0) | 0 |
| (1,0) | (1,1) | 1 |
| (0,1) | (1,1) | 1 |
| (1,1) | (0,1) | 0 |
下面咱們試着用感知機的表示方法(明確地顯示神經元)來表示這個異或門,結果如圖 2-11 所示。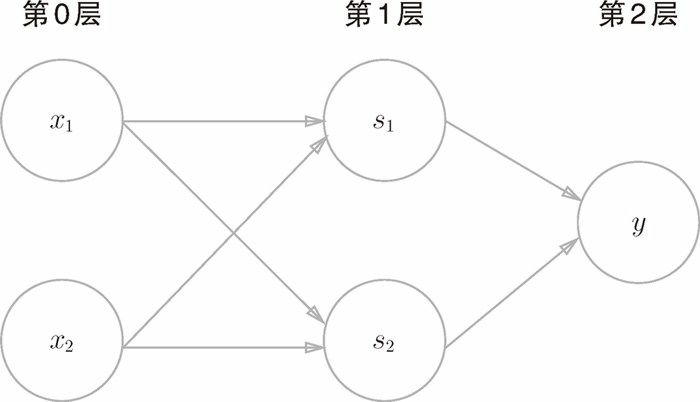
如圖 2-11 所示,異或門是一種多層結構的神經網絡。這裏,將最左邊的一列稱爲第 0 層,中間的一列稱爲第 1 層,最右邊的一列稱爲第 2 層。
圖 2-13 所示的感知機與前面介紹的與門、或門的感知機(圖2-1)形狀不一樣。實際上,與門、或門是單層感知機,而異或門是2層感知機。疊加了多層的感知機也稱爲多層感知機 (multi-layered perceptron)。
圖 2-11 中的感知機總共由 3 層構成,可是由於擁有權重的層實質上只有 2 層(第 0 層和第 1 層之間,第 1 層和第 2 層之間),因此稱爲「2 層感知機」。不過,有的文獻認爲圖 2-13 的感知機是由 3 層構成的,於是將其稱爲「3 層感知機」。
在圖 2-13 所示的 2 層感知機中,先在第 0 層和第 1 層的神經元之間進行信號的傳送和接收,而後在第 1 層和第 2 層之間進行信號的傳送和接收,具體以下所示。
- 第 0 層的兩個神經元接收輸入信號,並將信號發送至第 1 層的神經元。
- 第 1 層的神經元將信號發送至第 2 層的神經元,第 2 層的神經元輸出 y 。
2.5 總結
- 感知機是具備輸入和輸出的算法。給定一個輸入後,將輸出一個既定的值。
- 感知機將權重和偏置設定爲參數。
- 使用感知機能夠表示與門和或門等邏輯電路。
- 異或門沒法經過單層感知機來表示。
- 使用2層感知機能夠表示異或門。
- 單層感知機只能表示線性空間,而多層感知機能夠表示非線性空間。
- 1. 深度學習 感知器
- 2. 深度學習--感知器
- 3. 深度學習-感知器(感知機)
- 4. 零基礎入門深度學習 | 第一章:感知器
- 5. [筆記]《零基礎入門深度學習(1)-感知器》
- 6. 【轉載】零基礎入門深度學習(1) - 感知器
- 7. 深度學習入門基礎教程(一) 感知器
- 8. 零基礎入門深度學習(1) - 感知器
- 9. 零基礎入門深度學習(1)----感知器
- 10. 深度學習筆記(一)——感知器
- 更多相關文章...
- • Kotlin 基礎語法 - Kotlin 教程
- • Scala 基礎語法 - Scala教程
- • Kotlin學習(二)基本類型
- • Kotlin學習(一)基本語法
-
每一个你不满意的现在,都有一个你没有努力的曾经。
- 1. vs2019運行opencv圖片顯示代碼時,窗口亂碼
- 2. app自動化 - 元素定位不到?別慌,看完你就能解決
- 3. 在Win8下用cisco ××× Client連接時報Reason 422錯誤的解決方法
- 4. eclipse快速補全代碼
- 5. Eclipse中Java/Html/Css/Jsp/JavaScript等代碼的格式化
- 6. idea+spring boot +mabitys(wanglezapin)+mysql (1)
- 7. 勒索病毒發生變種 新文件名將帶有「.UIWIX」後綴
- 8. 【原創】Python 源文件編碼解讀
- 9. iOS9企業部署分發問題深入瞭解與解決
- 10. 安裝pytorch報錯CondaHTTPError:******