數論概論學習筆記（一）——勾股數

版權聲明：本文爲博主原創文章，未經博主容許不得轉載。

Pythagoras theorem（勾股定理）

一個直角三角形中，兩個直角邊邊長的平方加起來等於斜邊長的平方。 若是設直角三角形的兩條直角邊長度分別是a和b，斜邊長度是c，那麼能夠用數學語言表達：


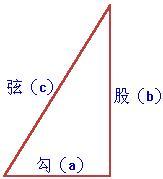
a2+b2=c2

知足這個等式且沒有公因數的的三元數組（a,b,c）稱爲勾股數。 可證a、b兩個數必然一奇一偶，證實以下： 若是數a,b都是奇數，則數c必爲偶數。可設a=2x+1,b=2y+1,c=2z,有

(2x+1)2+(2y+1)2=(2z)2

展開化簡獲得下式：

2x2+2x+2y2+2y+1=2z2

上式左邊爲奇數，右邊爲偶數，等式顯然不成立； 若是數a，b都是偶數，意味着c也是偶數。此時a,b,c均可以被2整除，此時a,b,c不互質。 證畢。 ———-

定理

由 a2+b2=c2 可得 a2=(c−b)(c+b)
  假設存在一個數d是(c-b),(c+b)的公因數，即d能夠整除(c-b)和(c+b)，則d也能夠整除

（c+b）+（c-b）= 2c 與 （c+b）-（c-b）= 2b

  故d整除2b和2c.而b、c沒有公因數，由於咱們假設（a,b,c）爲本原勾股數組，能夠得出d必定是1或2。但d也整除 (c+b)(c−b)=a2 且a爲奇數，因此d只能爲1，因此(c-b),(c+b)沒有公因數。
   如今咱們知道c-b與c+b沒有公因數且 a2=(c−b)(c+b) ,因此c-b,c+b的積是平方數，當且僅當c-b和c+b自己都是平方數。記

c+b=s2 , c−b=t2
其中 s>t⩾1 爲沒有公因數的奇數。關於b和c解方程組得

c=s2+t22 , b=s2−t22

因而                     a=(c+b)(c−b)−−−−−−−−−−−√=st

因此有如下定理

Pythagorean Triples  Theorem：
    We will get every primitive Pythagorean triple(a,b,c) with a odd and b even by using the formulas:

a=st ， b=s2−t22 ， c=s2+t22 ( s>t⩾1 )

經過這個公式，取不一樣s，t的值即可生成不一樣的勾股數。

下表爲 s⩽9 的全部勾股數

s	t	a=st	b=s2−t22	c=s2+t22
3	1	3	4	5
5	1	5	12	13
7	1	7	24	25
9	1	9	40	41
5	3	15	8	17
7	3	21	20	29
7	5	35	12	37
9	5	45	28	53
9	7	63	16	65