面經手冊 · 第4篇《HashMap數據插入、查找、刪除、遍歷,源碼分析》

做者:小傅哥
博客:https://bugstack.cnhtml
沉澱、分享、成長,讓本身和他人都能有所收穫!😄
1、前言
在上一章節咱們講解並用數據驗證了,HashMap中的,散列表的實現、擾動函數、負載因子以及擴容拆分等核心知識點以及相應的做用。java
除了以上這些知識點外,HashMap還有基本的數據功能;存儲、刪除、獲取、遍歷,在這些功能中常常會聽到鏈表、紅黑樹、之間轉換等功能。而紅黑樹是在jdk1.8引入到HashMap中解決鏈表過長問題的,簡單說當鏈表長度>=8時,將鏈表轉換位紅黑樹(固然這裏還有一個擴容的知識點,不必定都會樹化[MIN_TREEIFY_CAPACITY])。node
那麼本章節會進行講解如下知識點;程序員
- 數據插入流程和源碼分析
- 鏈表樹化以及樹轉鏈表
- 遍歷過程當中的無序Set的核心知識
🕵注意: 建議閱讀上一篇後,再閱讀本篇文章《HashMap核心知識,擾動函數、負載因子、擴容鏈表拆分,深度學習》面試
2、HashMap源碼分析
1. 插入
1.1 疑問點&考題
經過上一章節的學習:《HashMap核心知識,擾動函數、負載因子、擴容鏈表拆分,深度學習》 數組
你們對於一個散列表數據結構的HashMap往裏面插入數據時,基本已經有了一個印象。簡單來講就是經過你的Key值取得哈希再計算下標,以後把相應的數據存放到裏面。微信
但再這個過程當中會遇到一些問題,好比;數據結構
- 若是出現哈希值計算的下標碰撞了怎麼辦?
- 若是碰撞了是擴容數組仍是把值存成鏈表結構,讓一個節點有多個值存放呢?
- 若是存放的數據的鏈表過長,就失去了散列表的性能了,怎麼辦呢?
- 若是想解決鏈表過長,何時使用樹結構呢,使用哪一種樹呢?
這些疑問點都會在後面的內容中逐步講解,也能夠本身思考一下,若是是你來設計,你會怎麼作。app
1.2 插入流程和源碼分析
HashMap插入數據流程圖函數
visio原版流程圖,能夠經過關注公衆號:bugstack蟲洞棧,進行下載
以上就是HashMap中一個數據插入的總體流程,包括了;計算下標、什麼時候擴容、什麼時候鏈表轉紅黑樹等,具體以下;
- 首先進行哈希值的擾動,獲取一個新的哈希值。
(key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16); 判斷tab是否位空或者長度爲0,若是是則進行擴容操做。
if ((tab = table) == null || (n = tab.length) == 0) n = (tab = resize()).length;- 根據哈希值計算下標,若是對應小標正好沒有存放數據,則直接插入便可不然須要覆蓋。
tab[i = (n - 1) & hash]) - 判斷tab[i]是否爲樹節點,不然向鏈表中插入數據,是則向樹中插入節點。
- 若是鏈表中插入節點的時候,鏈表長度大於等於8,則須要把鏈表轉換爲紅黑樹。
treeifyBin(tab, hash); - 最後全部元素處理完成後,判斷是否超過閾值;
threshold,超過則擴容。 treeifyBin,是一個鏈表轉樹的方法,但不是全部的鏈表長度爲8後都會轉成樹,還須要判斷存放key值的數組桶長度是否小於64MIN_TREEIFY_CAPACITY。若是小於則須要擴容,擴容後鏈表上的數據會被拆分散列的相應的桶節點上,也就把鏈表長度縮短了。
JDK1.8 HashMap的put方法源碼以下:
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
// 初始化桶數組 table,table 被延遲到插入新數據時再進行初始化
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
// 若是桶中不包含鍵值對節點引用,則將新鍵值對節點的引用存入桶中便可
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
// 若是鍵的值以及節點 hash 等於鏈表中的第一個鍵值對節點時,則將 e 指向該鍵值對
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
// 若是桶中的引用類型爲 TreeNode,則調用紅黑樹的插入方法
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
// 對鏈表進行遍歷,並統計鏈表長度
for (int binCount = 0; ; ++binCount) {
// 鏈表中不包含要插入的鍵值對節點時,則將該節點接在鏈表的最後
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
// 若是鏈表長度大於或等於樹化閾值,則進行樹化操做
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
// 條件爲 true,表示當前鏈表包含要插入的鍵值對,終止遍歷
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
// 判斷要插入的鍵值對是否存在 HashMap 中
if (e != null) { // existing mapping for key
V oldValue = e.value;
// onlyIfAbsent 表示是否僅在 oldValue 爲 null 的狀況下更新鍵值對的值
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
// 鍵值對數量超過閾值時,則進行擴容
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
1.3 擴容機制
HashMap是基於數組+鏈表和紅黑樹實現的,但用於存放key值得的數組桶的長度是固定的,由初始化決定。
那麼,隨着數據的插入數量增長以及負載因子的做用下,就須要擴容來存放更多的數據。而擴容中有一個很是重要的點,就是jdk1.8中的優化操做,能夠不須要再從新計算每個元素的哈希值,這在上一章節中已經講到,能夠閱讀系列專題文章,機制以下圖;
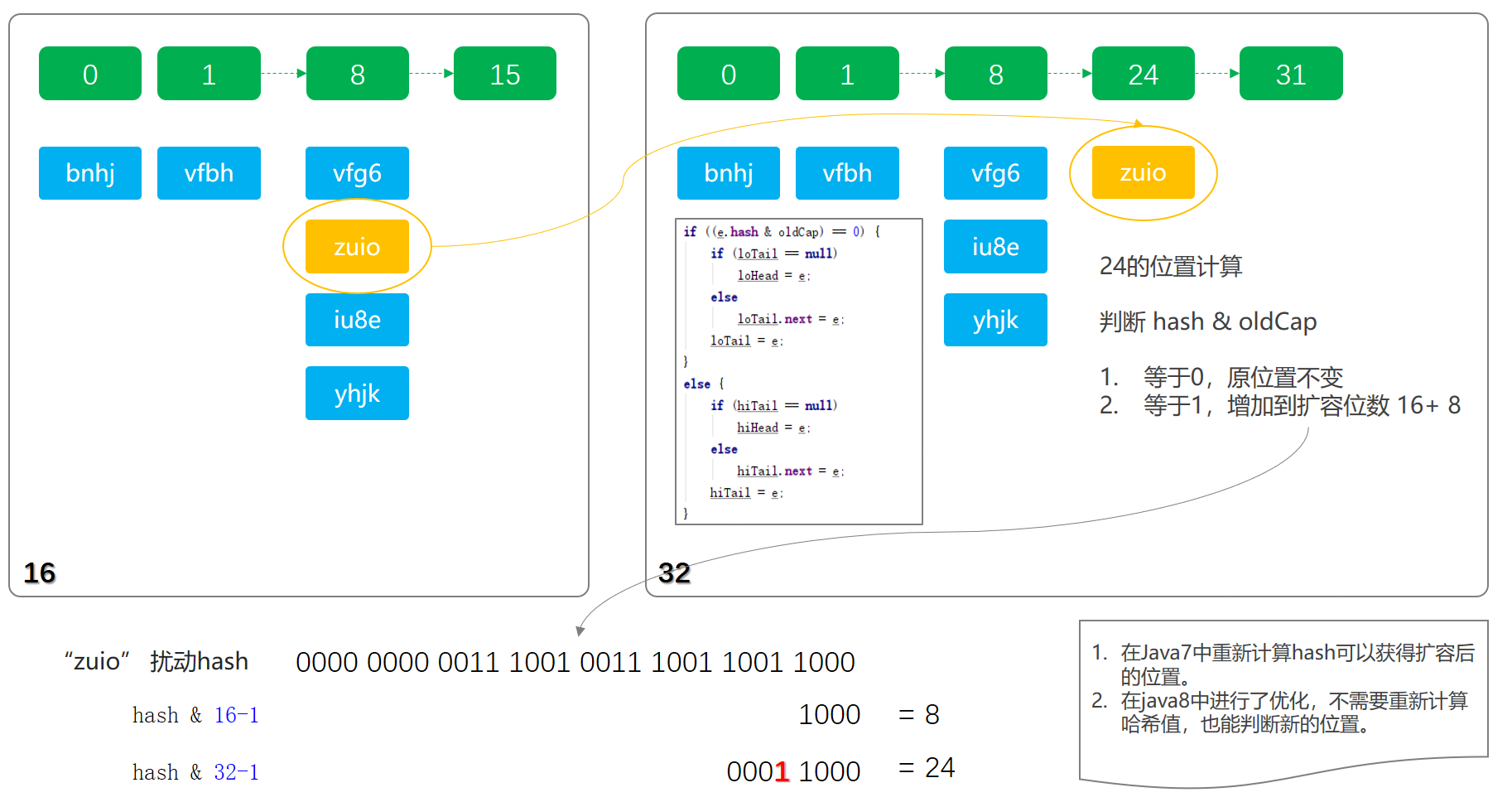
裏咱們主要看下擴容的代碼(註釋部分);
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
// Cap 是 capacity 的縮寫,容量。若是容量不爲空,則說明已經初始化。
if (oldCap > 0) {
// 若是容量達到最大1 << 30則再也不擴容
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
// 按舊容量和閥值的2倍計算新容量和閥值
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // double threshold
}
else if (oldThr > 0) // initial capacity was placed in threshold
// initial capacity was placed in threshold 翻譯過來的意思,以下;
// 初始化時,將 threshold 的值賦值給 newCap,
// HashMap 使用 threshold 變量暫時保存 initialCapacity 參數的值
newCap = oldThr;
else { // zero initial threshold signifies using defaults
// 這一部分也是,源代碼中也有相應的英文註釋
// 調用無參構造方法時,數組桶數組容量爲默認容量 1 << 4; aka 16
// 閥值;是默認容量與負載因子的乘積,0.75
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
// newThr爲0,則使用閥值公式計算容量
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
// 初始化數組桶,用於存放key
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
if (oldTab != null) {
// 若是舊數組桶,oldCap有值,則遍歷將鍵值映射到新數組桶中
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode)
// 這裏split,是紅黑樹拆分操做。在從新映射時操做的。
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // preserve order
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
// 這裏是鏈表,若是當前是按照鏈表存放的,則將鏈表節點按原順序進行分組{這裏有專門的文章介紹,如何不須要從新計算哈希值進行拆分《HashMap核心知識,擾動函數、負載因子、擴容鏈表拆分,深度學習》}
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
// 將分組後的鏈表映射到桶中
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
以上的代碼稍微有些長,可是總體的邏輯仍是蠻清晰的,主要包括;
- 擴容時計算出新的newCap、newThr,這是兩個單詞的縮寫,一個是Capacity ,另外一個是閥Threshold
- newCap用於創新的數組桶
new Node[newCap]; - 隨着擴容後,原來那些由於哈希碰撞,存放成鏈表和紅黑樹的元素,都須要進行拆分存放到新的位置中。
1.4 鏈表樹化
HashMap這種散列表的數據結構,最大的性能在於能夠O(1)時間複雜度定位到元素,但由於哈希碰撞不得已在一個下標裏存放多組數據,那麼jdk1.8以前的設計只是採用鏈表的方式進行存放,若是須要從鏈表中定位到數據時間複雜度就是O(n),鏈表越長性能越差。由於在jdk1.8中把過長的鏈表也就是8個,優化爲自平衡的紅黑樹結構,以此讓定位元素的時間複雜度優化近似於O(logn),這樣來提高元素查找的效率。但也不是徹底拋棄鏈表,由於在元素相對很少的狀況下,鏈表的插入速度更快,因此綜合考慮下設定閾值爲8才進行紅黑樹轉換操做。
鏈表轉紅黑樹,以下圖;
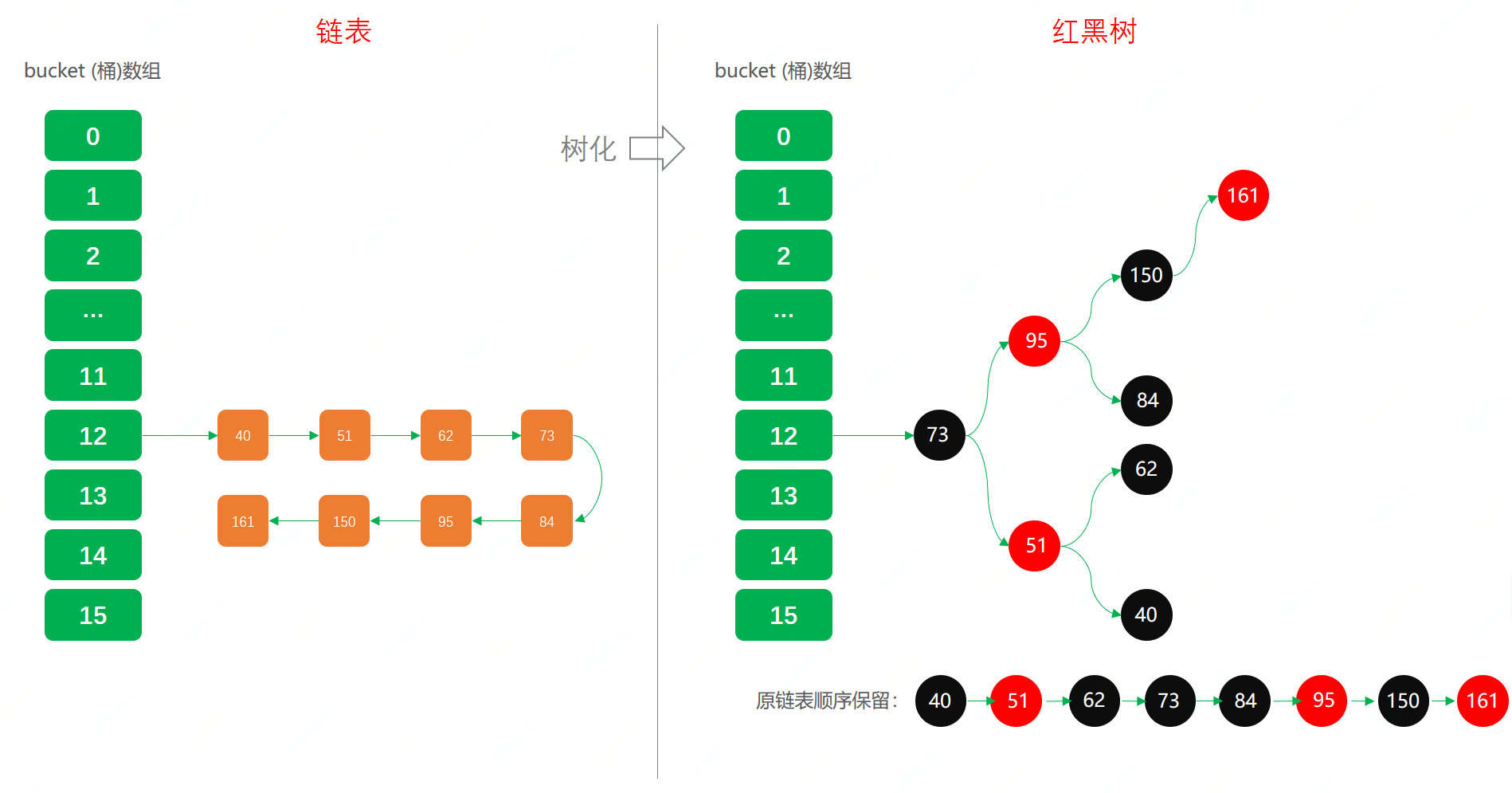
以上就是一組鏈表轉換爲紅黑樹的狀況,元素包括;40、5一、6二、7三、8四、9五、150、161 這些是通過實際驗證可分配到Idx:12的節點
經過這張圖,基本能夠有一個鏈表換行到紅黑樹的印象,接下來閱讀下對應的源碼。
鏈表樹化源碼
final void treeifyBin(Node<K,V>[] tab, int hash) {
int n, index; Node<K,V> e;
// 這塊就是咱們上面提到的,不必定樹化還可能只是擴容。主要桶數組容量是否小於64 MIN_TREEIFY_CAPACITY
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
resize();
else if ((e = tab[index = (n - 1) & hash]) != null) {
// 又是單詞縮寫;hd = head (頭部),tl = tile (結尾)
TreeNode<K,V> hd = null, tl = null;
do {
// 將普通節點轉換爲樹節點,但此時還不是紅黑樹,也就是說還不必定平衡
TreeNode<K,V> p = replacementTreeNode(e, null);
if (tl == null)
hd = p;
else {
p.prev = tl;
tl.next = p;
}
tl = p;
} while ((e = e.next) != null);
if ((tab[index] = hd) != null)
// 轉紅黑樹操做,這裏須要循環比較,染色、旋轉。關於紅黑樹,在下一章節詳細講解
hd.treeify(tab);
}
}
這一部分鏈表樹化的操做並不複雜,複雜點在於下一層的紅黑樹轉換上,這部分知識點會在後續章節中專門介紹;
以上源碼主要包括的知識點以下;
- 鏈表樹化的條件有兩點;鏈表長度大於等於八、桶容量大於64,不然只是擴容,不會樹化。
- 鏈表樹化的過程當中是先由鏈表轉換爲樹節點,此時的樹可能不是一顆平衡樹。同時在樹轉換過程當中會記錄鏈表的順序,
tl.next = p,這主要方便後續樹轉鏈表和拆分更方便。 - 鏈表轉換成樹完成後,在進行紅黑樹的轉換。先簡單介紹下,紅黑樹的轉換須要染色和旋轉,以及比對大小。在比較元素的大小中,有一個比較有意思的方法,
tieBreakOrder加時賽,這主要是由於HashMap沒有像TreeMap那樣自己就有Comparator的實現。
1.5 紅黑樹轉鏈
在鏈表轉紅黑樹中咱們重點介紹了一句,在轉換樹的過程當中,記錄了原有鏈表的順序。
那麼,這就簡單了,紅黑樹轉鏈表時候,直接把TreeNode轉換爲Node便可,源碼以下;
final Node<K,V> untreeify(HashMap<K,V> map) {
Node<K,V> hd = null, tl = null;
// 遍歷TreeNode
for (Node<K,V> q = this; q != null; q = q.next) {
// TreeNode替換Node
Node<K,V> p = map.replacementNode(q, null);
if (tl == null)
hd = p;
else
tl.next = p;
tl = p;
}
return hd;
}
// 替換方法
Node<K,V> replacementNode(Node<K,V> p, Node<K,V> next) {
return new Node<>(p.hash, p.key, p.value, next);
}
由於記錄了鏈表關係,因此替換過程很容易。因此好的數據結構可讓操做變得更加容易。
2. 查找
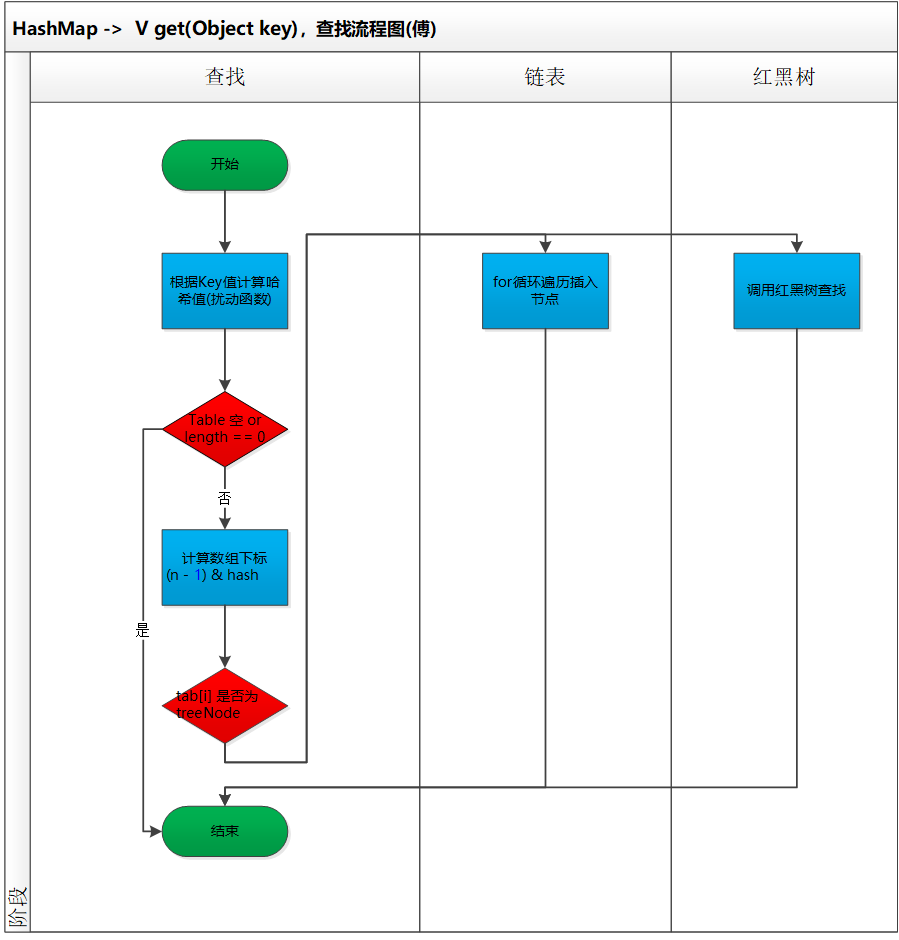
上圖就是HashMap查找的一個流程圖,仍是比較簡單的,同時也是高效的。
接下來咱們在結合代碼,來分析這段流程,以下;
public V get(Object key) {
Node<K,V> e;
// 一樣須要通過擾動函數計算哈希值
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
// 判斷桶數組的是否爲空和長度值
if ((tab = table) != null && (n = tab.length) > 0 &&
// 計算下標,哈希值與數組長度-1
(first = tab[(n - 1) & hash]) != null) {
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k))))
return first;
if ((e = first.next) != null) {
// TreeNode 節點直接調用紅黑樹的查找方法,時間複雜度O(logn)
if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
// 若是是鏈表就依次遍歷查找
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}
以上查找的代碼仍是比較簡單的,主要包括如下知識點;
- 擾動函數的使用,獲取新的哈希值,這在上一章節已經講過
- 下標的計算,一樣也介紹過
tab[(n - 1) & hash]) - 肯定了桶數組下標位置,接下來就是對紅黑樹和鏈表進行查找和遍歷操做了
3. 刪除
public V remove(Object key) {
Node<K,V> e;
return (e = removeNode(hash(key), key, null, false, true)) == null ?
null : e.value;
}
final Node<K,V> removeNode(int hash, Object key, Object value,
boolean matchValue, boolean movable) {
Node<K,V>[] tab; Node<K,V> p; int n, index;
// 定位桶數組中的下標位置,index = (n - 1) & hash
if ((tab = table) != null && (n = tab.length) > 0 &&
(p = tab[index = (n - 1) & hash]) != null) {
Node<K,V> node = null, e; K k; V v;
// 若是鍵的值與鏈表第一個節點相等,則將 node 指向該節點
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
node = p;
else if ((e = p.next) != null) {
// 樹節點,調用紅黑樹的查找方法,定位節點。
if (p instanceof TreeNode)
node = ((TreeNode<K,V>)p).getTreeNode(hash, key);
else {
// 遍歷鏈表,找到待刪除節點
do {
if (e.hash == hash &&
((k = e.key) == key ||
(key != null && key.equals(k)))) {
node = e;
break;
}
p = e;
} while ((e = e.next) != null);
}
}
// 刪除節點,以及紅黑樹須要修復,由於刪除後會破壞平衡性。鏈表的刪除更加簡單。
if (node != null && (!matchValue || (v = node.value) == value ||
(value != null && value.equals(v)))) {
if (node instanceof TreeNode)
((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
else if (node == p)
tab[index] = node.next;
else
p.next = node.next;
++modCount;
--size;
afterNodeRemoval(node);
return node;
}
}
return null;
}
- 刪除的操做也比較簡單,這裏面都沒有太多的複雜的邏輯。
- 另外紅黑樹的操做由於被包裝了,只看使用上也是很容易。
4. 遍歷
4.1 問題點
HashMap中的遍歷也是很是經常使用的API方法,包括;
KeySet
for (String key : map.keySet()) {
System.out.print(key + " ");
}
EntrySet
for (HashMap.Entry entry : map.entrySet()) {
System.out.print(entry + " ");
}
從方法上以及平常使用都知道,KeySet是遍歷是無序的,但每次使用不一樣方式遍歷包括keys.iterator(),它們遍歷的結果是固定的。
那麼從實現的角度來看,這些種遍歷都是從散列表中的鏈表和紅黑樹獲取集合值,那麼他們有一個什麼固定的規律嗎?
4.2 用代碼測試
測試的場景和前提;
- 這裏咱們要設定一個既有紅黑樹又有鏈表結構的數據場景
- 爲了能夠有這樣的數據結構,咱們最好把HashMap的初始長度設定爲64,避免在鏈表超過8位後擴容,而是直接讓其轉換爲紅黑樹。
找到18個元素,分別放在不一樣節點(這些數據經過程序計算得來);
- 桶數組02節點:2四、4六、68
- 桶數組07節點:29
- 桶數組12節點:150、17二、19四、27一、29三、370、39二、49一、590
代碼測試
@Test
public void test_Iterator() {
Map<String, String> map = new HashMap<String, String>(64);
map.put("24", "Idx:2");
map.put("46", "Idx:2");
map.put("68", "Idx:2");
map.put("29", "Idx:7");
map.put("150", "Idx:12");
map.put("172", "Idx:12");
map.put("194", "Idx:12");
map.put("271", "Idx:12");
System.out.println("排序01:");
for (String key : map.keySet()) {
System.out.print(key + " ");
}
map.put("293", "Idx:12");
map.put("370", "Idx:12");
map.put("392", "Idx:12");
map.put("491", "Idx:12");
map.put("590", "Idx:12");
System.out.println("\n\n排序02:");
for (String key : map.keySet()) {
System.out.print(key + " ");
}
map.remove("293");
map.remove("370");
map.remove("392");
map.remove("491");
map.remove("590");
System.out.println("\n\n排序03:");
for (String key : map.keySet()) {
System.out.print(key + " ");
}
}
這段代碼分別測試了三種場景,以下;
- 添加元素,在HashMap仍是隻鏈表結構時,輸出測試結果01
- 添加元素,在HashMap轉換爲紅黑樹時候,輸出測試結果02
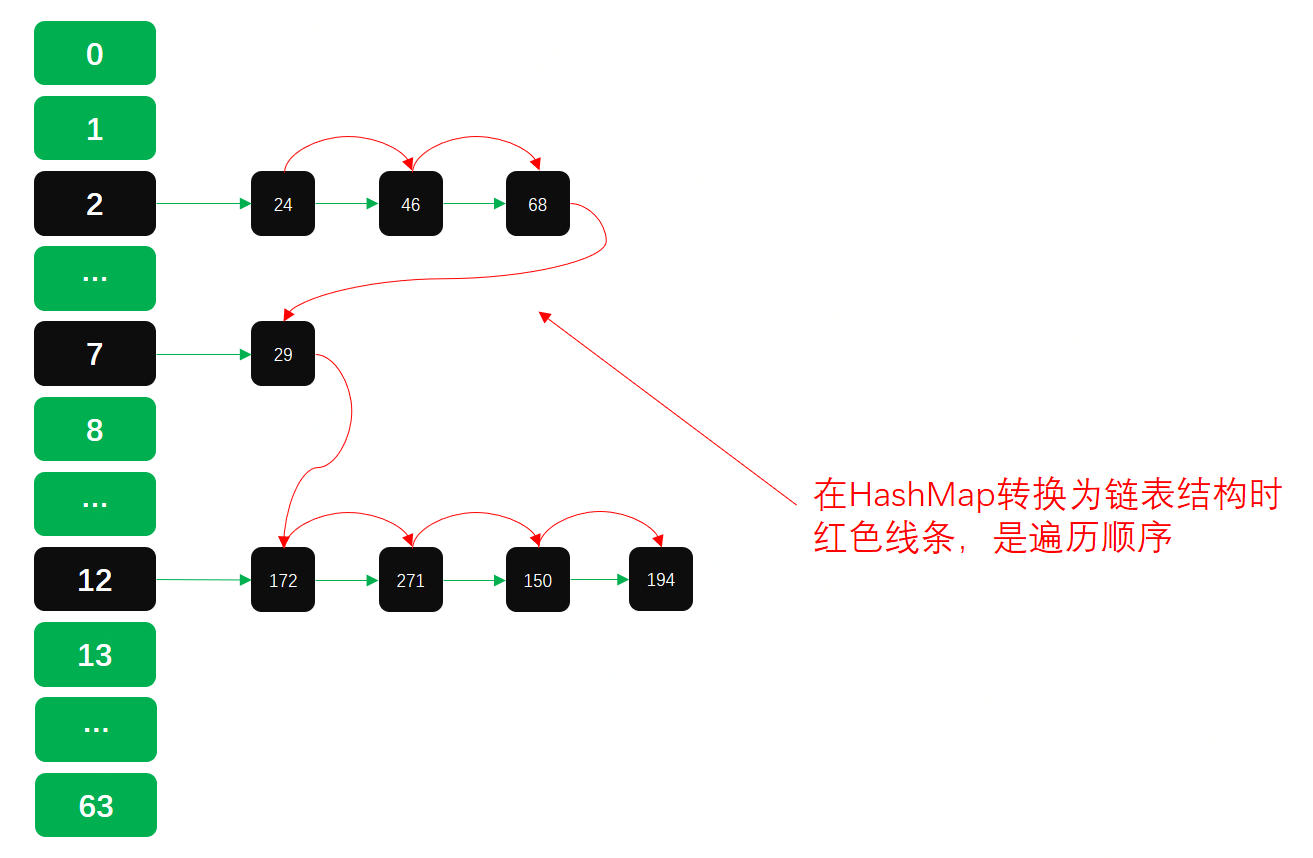
- 刪除元素,在HashMap轉換爲鏈表結構時,輸出測試結果03
4.3 測試結果分析
排序01: 24 46 68 29 150 172 194 271 排序02: 24 46 68 29 271 150 172 194 293 370 392 491 590 排序03: 24 46 68 29 172 271 150 194 Process finished with exit code 0
從map.keySet()測試結果能夠看到,以下信息;
- 01狀況下,排序定位哈希值下標和鏈表信息

- 02狀況下,由於鏈表轉換爲紅黑樹,樹根會移動到數組頭部。
moveRootToFront()方法

- 03狀況下,由於刪除了部分元素,紅黑樹退化成鏈表。
3、總結
- 這一篇API源碼以及邏輯與上一篇數據結構中擾動函數、負載因子、散列表實現等,內容的結合,算是把HashMap基本經常使用技術點,梳理完成了。但知識毫不止於此,這裏還有紅黑樹的相關技術內容,後續會進行詳細。
- 除了HashMap之外還有TreeMap、ConcurrentHashMap等,每個核心類都有一些相關的核心知識點,每個都很是值得深刻研究。這個燒腦的過程,是學習得到知識的最佳方式。
- 可能關於HashMap還有一些疏漏的點,也但願閱讀的小夥伴能夠提出更多的問題,互相學習,共同進步,本文就到這裏,感謝您的閱讀!
4、推薦閱讀
- 1. Trie樹,插入,查找,刪除,遍歷
- 2. 單鏈表的插入、刪除、遍歷(查找||改寫數據)
- 3. java實現二叉查找樹(插入、刪除、遍歷、查找)
- 4. C++ 二叉查找樹 —— 插入、遍歷、查找、刪除、銷燬
- 5. 單鏈表創建,插入,刪除,查找,遍歷操做
- 6. 二叉搜索樹Java實現(查找、插入、刪除、遍歷)
- 7. 基本數據結構 -- 鏈表的遍歷、查找、插入和刪除
- 8. C語言 AVL平衡二叉查找樹 插入/刪除/遍歷/查找
- 9. HashMap 源碼分析(刪除+總結)JDK1.8
- 10. 基本數據結構 -- 二叉查找樹的插入、刪除、查找和遍歷
- 更多相關文章...
- • PHP MySQL 插入數據 - PHP教程
- • Eclipse 查找 - Eclipse 教程
- • 算法總結-二分查找法
- • C# 中 foreach 遍歷的用法
-
每一个你不满意的现在,都有一个你没有努力的曾经。
- 1. vs2019運行opencv圖片顯示代碼時,窗口亂碼
- 2. app自動化 - 元素定位不到?別慌,看完你就能解決
- 3. 在Win8下用cisco ××× Client連接時報Reason 422錯誤的解決方法
- 4. eclipse快速補全代碼
- 5. Eclipse中Java/Html/Css/Jsp/JavaScript等代碼的格式化
- 6. idea+spring boot +mabitys(wanglezapin)+mysql (1)
- 7. 勒索病毒發生變種 新文件名將帶有「.UIWIX」後綴
- 8. 【原創】Python 源文件編碼解讀
- 9. iOS9企業部署分發問題深入瞭解與解決
- 10. 安裝pytorch報錯CondaHTTPError:******