那麼，Prolog，告訴我怎麼走

今年四月左右，我心血來潮地爲本身立了一個學習Prolog的目標——對，就是那門以邏輯編程和人工智能爲賣點的語言。不只要學會它的基本用法，還妄想用它像朋友圈廣告裏的Python那樣，用來處理Excel文件中的大數據！

儘管處理大數據是開個玩笑，但學習Prolog的目標是真的。既然要學習一門編程語言，就必須找一本靠譜的教材。在無中生友以後，我選擇了由譚浩強老先生主編的《Learn Prolog Now》做爲入門讀物。

儘管《Learn Prolog Now》的內容一點也不real world，卻按部就班、很是地適合初學者，每一章的結尾還準備了「上機題」。出人意料的是，僅僅在第三章就遇到了不會作的題目。在焦急地苦戰一番未果後，我拖着疲憊的身軀擱置了它，繼續學習後面的章節。

時隔五個月，我再次嘗試解答這道題目。卻驚喜地發現，只須要冷靜地分析再仔細運用前三章學過的知識，解決這道題目也就是水到渠成的事情了。

因此究竟是個什麼題？

講了這麼多，是時候揭曉這它的真面目了。因爲第三題以第二題爲基礎，所以一併搬運了過來

感興趣的朋友也能夠直接移步源網頁查看。

看完上面的題目，只學過主流編程語言的朋友大概會是一頭霧水，畢竟不管是代碼仍是術語，都與平日裏使用的截然不同。我來試着解釋一下。像byCar(auckland, hamilton)和byTrain(metz, frankfurt)這樣的代碼，用Prolog的術語來說叫作「事實」。就像數學中的公理同樣，它們老是成立的。若是向Prolog提問，它會給出確定的回答

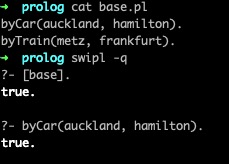
byCar和byTrain被稱爲「謂詞」，auckland和hamilton則是「原子」。

第二題要求定義travel/2，第三題要求定義travel/3。travel是謂詞的名字，2和3則是它所接受的參數的個數。定義一個謂詞就是給出描述它什麼時候成立的「規則」，舉個例子，能夠定義一個名爲len的謂詞，只有當第二個參數等於第一個參數的長度時才成立

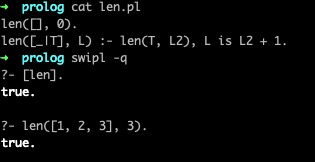
以大寫字母開頭的標識符（如題目中的X，上圖中的T、L）是變量，在歸一化（unification）時Prolog可以爲它們賦值使得查詢成立。

鑑於本文不是Prolog的入門教程，各位讀者若是想進一步瞭解Prolog，還請移步《Learn Prolog Now》的相關章節。

先解決第二題吧

講了這麼多，該進入正題了。第二題其實不難，細心的讀者應該已經發現，這題能夠用遞歸來解決（就像上文的len同樣）。

設謂詞travel的兩個參數分別叫作S和E，各表明起點和終點。顯然，travel(S, E)成立，當且僅當：

1. 能夠從S搭乘汽車（byCar）、火車（byTrain），或飛機（byPlane）抵達E，或者；
2. 存在另外一個城市M，能夠從S搭乘汽車、火車，或飛機抵達M，而且travel(M, E)也成立。

上述算法能夠輕鬆地寫成Prolog代碼

byCar(auckland,hamilton).
byCar(hamilton,raglan).
byCar(valmont,saarbruecken).
byCar(valmont,metz).

byTrain(metz,frankfurt).
byTrain(saarbruecken,frankfurt).
byTrain(metz,paris).
byTrain(saarbruecken,paris).

byPlane(frankfurt,bangkok).
byPlane(frankfurt,singapore).
byPlane(paris,losAngeles).
byPlane(bangkok,auckland).
byPlane(singapore,auckland).
byPlane(losAngeles,auckland).

travel(S, E) :- just_go(S, E).
travel(S, E) :- just_go(S, M), travel(M, E).

just_go(S, E) :- byCar(S, E).
just_go(S, E) :- byTrain(S, E).
just_go(S, E) :- byPlane(S, E).

讓Prolog告訴我們這個travel/2寫得對不對

精彩！

你話我猜？

Prolog不只知道一個查詢是否成立，還知道這個查詢在什麼參數下成立。例如，可讓Prolog告訴我們，從valmont能夠抵達哪一些城市，以及哪一些城市能夠抵達auckland

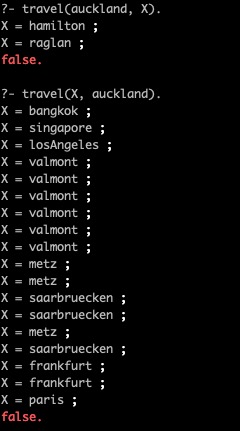
這正是在接下來的題目中須要發揚光大的能力。

終於來到第三題

第三題所要求的travel是一個接受三個參數的謂詞，第三個參數由從起點到終點的途徑城市構成。設這個新的變量爲R，那麼travel(S, E, R)成立當且僅當：

1. 能夠從S抵達E，而且R爲go(S, E)，或者；
2. 存在另外一個城市M，以及另外一條路徑R2。能夠從S抵達M，而且travel(M, E, R2)成立，而且R爲go(S, M, R2)。

那麼如何在規則中描述R的結構呢？莫非是像上面的謂詞len那樣，在:-的右側寫上形如R is go(S, M, R2)這樣的代碼？

並非。

藉助Prolog強大的模式匹配能力，只須要在:-的左邊聲明R的結構便可

byCar(auckland,hamilton).
byCar(hamilton,raglan).
byCar(valmont,saarbruecken).
byCar(valmont,metz).

byTrain(metz,frankfurt).
byTrain(saarbruecken,frankfurt).
byTrain(metz,paris).
byTrain(saarbruecken,paris).

byPlane(frankfurt,bangkok).
byPlane(frankfurt,singapore).
byPlane(paris,losAngeles).
byPlane(bangkok,auckland).
byPlane(singapore,auckland).
byPlane(losAngeles,auckland).

travel(S, E, go(S, E)) :- just_go(S, E).
travel(S, E, go(S, M, R)) :- just_go(S, M), travel(M, E, R).

just_go(S, E) :- byCar(S, E).
just_go(S, E) :- byTrain(S, E).
just_go(S, E) :- byPlane(S, E).

加載這段代碼後，就能讓Prolog告訴咱們，如何從valmont去往losAngeles了

Prolog不只找出了題目中所給出的答案（見上圖的第二行X =），還找出了另一條可行的路徑。

後記

確實不難，難怪能夠做爲第三章的習題。

閱讀原文