20162330 2017-2018-1《程序設計與數據結構》第九周學習總結

時間 2019-11-18

原文原文鏈接

2017-2018-1 學習總結目錄：　1　2　3　5　6　7　9　10　11　12
html

堆是一棵徹底二叉樹。（平衡、約束）node
分類：最大堆（大頂堆）、最小堆（小頂堆）。
git
基本操做：添加元素、找到最大值、刪除最大值。算法
添加元素：將元素添加爲新的葉結點，同時保持樹是徹底樹，將該元素向根的地方移動，將它與父結點對換，直到其中的元素大小關係知足要求爲止。api
找到最大元素：此操做較簡單，由於在添加元素的過程當中就已經把最大元素移動到了根位置。markdown
刪除最大元素：利用最後的葉結點來取代根，而後將其向下移動到合適的位置。數據結構
堆和二叉排序樹的區別：編輯器

1.堆是一棵徹底二叉樹，二叉排序樹不必定是徹底二叉樹；
2.在二叉排序樹中，某結點的右孩子結點的值必定大於該結點的左孩子結點的值，在堆中卻不必定；
3.在二叉排序樹中，最小值結點是最左下結點，最大值結點是最右下結點。在堆中卻不必定。學習

堆的實現

最大堆接口的實現：

public interface MaxHeap<T extends Comparable<T>> extends BinaryTree<T>
{
    //  Adds the specified object to the heap.
    public void add (T obj);

    //  Returns a reference to the element with the highest value in the heap.
    public T getMax ();

    //  Removes and returns the element with the highest value in the heap.
    public T removeMax ();
}

在 LinkedMaxHeap 中的 add 方法依賴於HeapNode中的兩個方法：getParentAdd 和 heapifyAdd 方法。
其中 getParentAdd 方法從樹的最後一個結點開始，一個一個檢測，尋找新加入結點的父結點。從樹中開始向上查找，直到發現它是某個結點的左子結點，或是到達根結點時爲止。若是到達根結點，新的父結點是根的左後繼結點。若是沒有到達根結點，則再查找右子結點的最左後繼。

public HeapNode<T> getParentAdd (HeapNode<T> last)
    {
        HeapNode<T> result = last;

        while ((result.parent != null) && (result.parent.left != result))
            result = result.parent;

        if (result.parent != null)
            if (result.parent.right == null)
                result = result.parent;
            else
            {
                result = (HeapNode<T>) result.parent.right;
                while (result.left != null)
                    result = (HeapNode<T>) result.left;
            }
        else
            while (result.left != null)
                result = (HeapNode<T>) result.left;

        return result;
    }

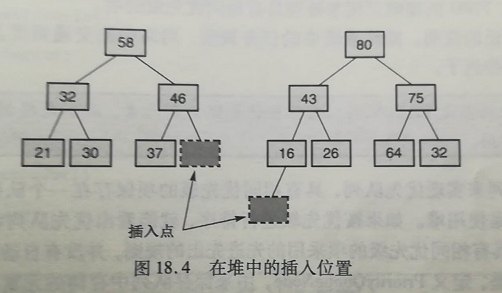![](http://images2017.cnblogs.com/blog/1062725/201711/1062725-20171105231918013-345760295.png)

一旦新的葉結點添加到樹中，heapifyAdd 方法就利用 parent 引用沿樹向上移動，必要時交換元素。（交換的是元素，不是結點）

public void heapifyAdd (HeapNode<T> last)
    {
        T temp;
        HeapNode<T> current = last;

        while ((current.parent != null) &&
                ((current.element).compareTo(current.parent.element) > 0))
        {
            temp = current.element;
            current.element = current.parent.element;
            current.parent.element = temp;
            current = current.parent;
        }
    }

堆排序

思路：將一組元素一項項地插入到堆中，而後一次刪除一個。由於最大元素最早從堆中刪除，因此一次次刪除獲得的元素將是有序序列，並且是降序的。同理，一個最小堆可用來獲得升序的排序結果。spa

優先隊列

兩個規則：

① 具備更高優先級的項排在前面。（不是FIFO）
② 具備相同優先級的項按先進先出的規則排列。（FIFO）
實現方法：定義結點類保存隊列中的元素、優先級和排列次序。而後，經過實現 Comparable 接口定義 compareTo 方法，先比較優先級，再比較排列次序。

【返回目錄】

教材學習中的問題和解決過程

【問題】：對於堆排序的詳細步驟（具體順序）不清楚，教材上也只提供了思路。
解決方案 ：（查找相關資料）
【步驟一】構造初始堆，以大頂堆爲例，給無序序列構造一個大頂堆，假設無序序列以下：

從最後一個非葉子結點開始（葉結點不用調整，第一個非葉子結點 arr.length/2-1=5/2-1=1，也就是下面的6結點），從左至右，從下至上進行調整：

找到第二個非葉節點4，因爲[4,9,8]中9元素最大，4和9交換。

這時，交換致使了子根[4,5,6]結構混亂，繼續調整，[4,5,6]中6最大，交換4和6。

這樣大頂堆就完成了。
【步驟二】將堆頂元素與末尾元素進行交換，使末尾元素最大。而後繼續調整堆，再將堆頂元素與末尾元素交換，獲得第二大元素。首先將堆頂元素9和末尾元素4進行交換：

從新調整結構，使其繼續知足堆定義：

再將堆頂元素8與末尾元素5進行交換，獲得第二大元素8：
【步驟三】如此反覆進行交換、重建、交換。反覆進行此過程，即可獲得有序序列：
因此，基本步驟歸納爲：將無序堆構建成大頂堆或小頂堆，再經過反覆交換堆頂元素和當前末尾元素並調整，最後使整個序列有序。

【返回目錄】

代碼調試中的問題和解決過程

【問題】：對於課本中出現的代碼錯誤問題。
解決方案：能夠參考張之睿的解答：

【返回目錄】

代碼託管

本週代碼上傳至 ch18 文件夾中：
（statistics.sh腳本的運行結果截圖）

上週考試錯題總結

【錯題1】Which of the following best describes a balanced tree?
A .A balanced trees has all nodes at exactly the same level.
B .A balanced tree has no nodes at exactly the same level.
C .A balanced tree has half of the nodes at one level and half the nodes at another level.
D .A balanced tree has all of the nodes within one level of each other.
E .none of the above correctly describe a balanced tree.
錯誤緣由：作第一遍的時候我選了D，可是第二遍覺得第一遍作錯了，認爲D只描述了平衡樹的一種狀況，不全面，因此錯選E。
加深理解：儘管樹的全部結點都是徹底相同的，但並非全部的平衡樹都具備這種特性。而D中的 within one level of each other 就至關於全部子結點彼此不超過一層。
【錯題2】In an inorder traversal, the elements of a tree are visited in order of their distance from the root.
A .true
B .false
錯誤緣由：這個題也是，第一遍我選了B，可是仔細一想感受是錯的，因而查了查 order 的意思，居然查到了「分治」的意思，我一想中序遍歷根結點在中間，就選了A。
加深理解：層序遍歷是根據元素與根之間的距離依次訪問的。

【返回目錄】

結對及互評

本週結對學習狀況

莫禮鍾本週狀態通常，娛樂時間仍是有些多，不過主動承擔了團隊中的交互工做，負責與其餘小組成員交流前幾周的團隊狀況，完成的不錯，還寫了總結。對於其餘內容的學習，有些斷斷續續，不夠連貫，不少方面還須要補一下，恰好我也有一些須要補充的內容，打算下週再抽出一部分時間學習，畢竟咱們的代碼實踐方面都比較弱，此次還要特別感謝莫禮鍾之前的結對夥伴 楊京典 可以在晚上抽空來指導莫禮鍾學習，主要是對於上次未完成實驗的補充學習。
20162319
- 結對學習內容
  - 實驗二樹
  - 哈夫曼樹

其餘（感悟、思考等，可選）

本週能夠說是忙綠而焦慮的一週，在經歷了上週的實驗以後，又恢復到教材內容學習的進程，本週的哈夫曼樹我是硬生生地「啃」下來的，我再次感覺到了數據結構的難度。多是個人代碼寫得太少，不少算法都是隻有思路而寫不出代碼，還有關於樹的內容我須要及時梳理一下。關於團隊項目，咱們又經歷了一次磨鍊，我用了一個下午的時間學會了如何使 markdown 文件轉換成 pdf 格式，而且又瞭解到幾個新的 markdown 編輯器，還實驗了一些碼雲上獨特而惱人的 markdown 格式，大概本週我在這上面花費的時間多一些吧。

【附1】教材及考試題中涉及到的英語：

Chinese	English	Chinese	English
退化的	degenerate	後繼承	successor
屬性	property	插圖	illustration

【附2】本週小組博客

【返回目錄】

學習進度條

	代碼行數（新增/累積）	博客量（新增/累積）	學習時間（新增/累積）	重要成長
目標	5000行	30篇	400小時
第一週	234/234	1/28	14/14	瞭解算法效率、大O符號等理論內容
第二週	255/489	1/29	12/26	瞭解敏捷的團隊、泛型的使用
第三週	436/925	2/31	10/36	瞭解一些查找和排序的算法
第四周	977/1902	3/34	10/46	掌握實現線性結構
第五週	800/2702	2/36	12/58	掌握實現棧集合
第六週	260/2962	1/37	8/64	掌握實現隊列集合
第七週	843/3805	4/41	12/76	掌握實現樹的基本結構
第八週	738/4543	1/42	12/88	二叉樹實驗（查找樹、平衡樹）
第九周	1488/6031	2/44	15/103	掌握堆的實現、哈夫曼樹基本結構