紅黑樹

紅黑樹

1. 紅黑樹的性質:

   • 性質 1：每一個節點要麼是紅色，要麼是黑色。
   • 性質 2：根節點永遠是黑色的。
   • 性質 3：全部的葉節點都是空節點（即 null），而且是黑色的。
   • 性質 4：每一個紅色節點的兩個子節點都是黑色。（從每一個葉子到根的路徑上不會有兩個連續的紅色節點）
   • 性質 5：從任一節點到其子樹中每一個葉子節點的路徑都包含相同數量的黑色節點。

2. black-height--紅黑樹從根節點到每一個葉子節點的路徑都包含相同數量的黑色節點，所以從根節點到葉子節點的路徑中包含的黑色節點數被稱爲樹的「黑色高度（black-height.

3. 因爲紅黑樹只是一個特殊的排序二叉樹，紅黑樹的插入刪除和排序二叉樹相同,只是影響了平衡性能,所以須要插入和刪除後修復.

4. 添加節點後修復:(有如下可知,基本上須要關心的是3,4,這是由於加如的新節點爲紅色,不能連續出現兩個紅色節點,破環了性質4,所以咱們須要修復的是不知足性質(4) (u-uncle;p-parent;g-grandparent爲下面用到的簡寫)
5. 新節點 N 是樹的根節點，沒有父節點---只需把此節點設置位黑色便可
6. 新節點的父節點 P 是黑色--無需操做
7. 父節點是祖父節點的左孩子且父節點爲紅色--此時,無論新加入的節點時左孩子仍是右孩子,明顯左邊過長,須要右旋.
   - 叔叔節點是紅色--------u,p變爲黑色,g變爲紅色,且繼續檢測g以上的節點是否知足,可能致使g顏色的變化引發上面節點不知足性質4,故須要將g設爲新的變化節點,繼續忘上進行調整.
   - 叔叔是黑色，且當前節點是右孩子---先左旋p,獲得下面的狀況,防止直接旋轉獲得右邊過長.
   - 叔叔是黑色，且當前節點是左孩子。--將p設爲黑色,將G設爲紅色,右旋.---此時,其父節點爲黑色,循環中止
8. 父節點是祖父節點的左孩子且父節點爲紅色--此時,無論新加入的節點時左孩子仍是右孩子,明顯左邊過長,須要左旋.
   • 叔叔節點是紅色-------u,p變爲黑色,g變爲紅色,且繼續檢測g以上的節點是否知足,可能致使g顏色的變化引發上面節點不知足性質4,故須要將g設爲新的變化節點,繼續忘上進行調整.
   • 叔叔是黑色，且當前節點是左孩子---先右旋,獲得下面的狀況,防止直接旋轉致使左邊過長
   • 叔叔是黑色，且當前節點是右孩子。--將p設爲黑色,將G設爲紅色,左旋.---此時,其父節點爲黑色,循環中止

插入及其修復代碼:

public void insert(Node node) {
    node.color = RED;
    Node cur = mroot;
    Node tmp = null;
    int num;

    //找到要插入的父節點
    while (cur != null) {
      tmp = cur;
      num = cmp.compare(tmp, node);
      cur = num > 0 ? tmp.left : tmp.right;
    }

    node.parent = tmp;
    if (tmp != null) {
      num = cmp.compare(tmp, node);
      if (num >= 0) {
        tmp.left = node;
      } else {
        tmp.right = node;
      }
    } else {
      mroot = node;
    }
    fixInsertRBT(node);
  }

private void fixInsertRBT(Node node) {
    Node p, g, u;
    //狀況3,4
    while (node.parent != null && node.parent.color == RED) {
      p = node.parent;
      g = p.parent;
      //狀況3:p爲g的左孩子
      if (p == g.left) {
        //g一定不會爲空當沒有祖父節點的時候就不會跳進此循環
        u = g.getRight();
        //若是p,u都爲紅色.
        if (u != null && u.color == RED) {
          p.color = BLACK;
          u.color = BLACK;
          g.color = RED;
          node = g;
        } else {
          //當node爲右孩子的時候,先左旋,使得不至於直接旋轉致使右邊過長,從而形成不平衡.
          if (node == p.right) {
            rotateLeft(p);
            Node tmp = p;
            p = node;
            node = tmp;
          }
          //當node 爲左孩子的時候
          p.color = BLACK;
          g.color = RED;
          rotateRight(g);
        }
      }
      //狀況4--p爲g的右孩子
      else {
        u = g.getLeft();
        if (u != null && u.color == RED) {
          p.setColor(BLACK);
          u.setColor(BLACK);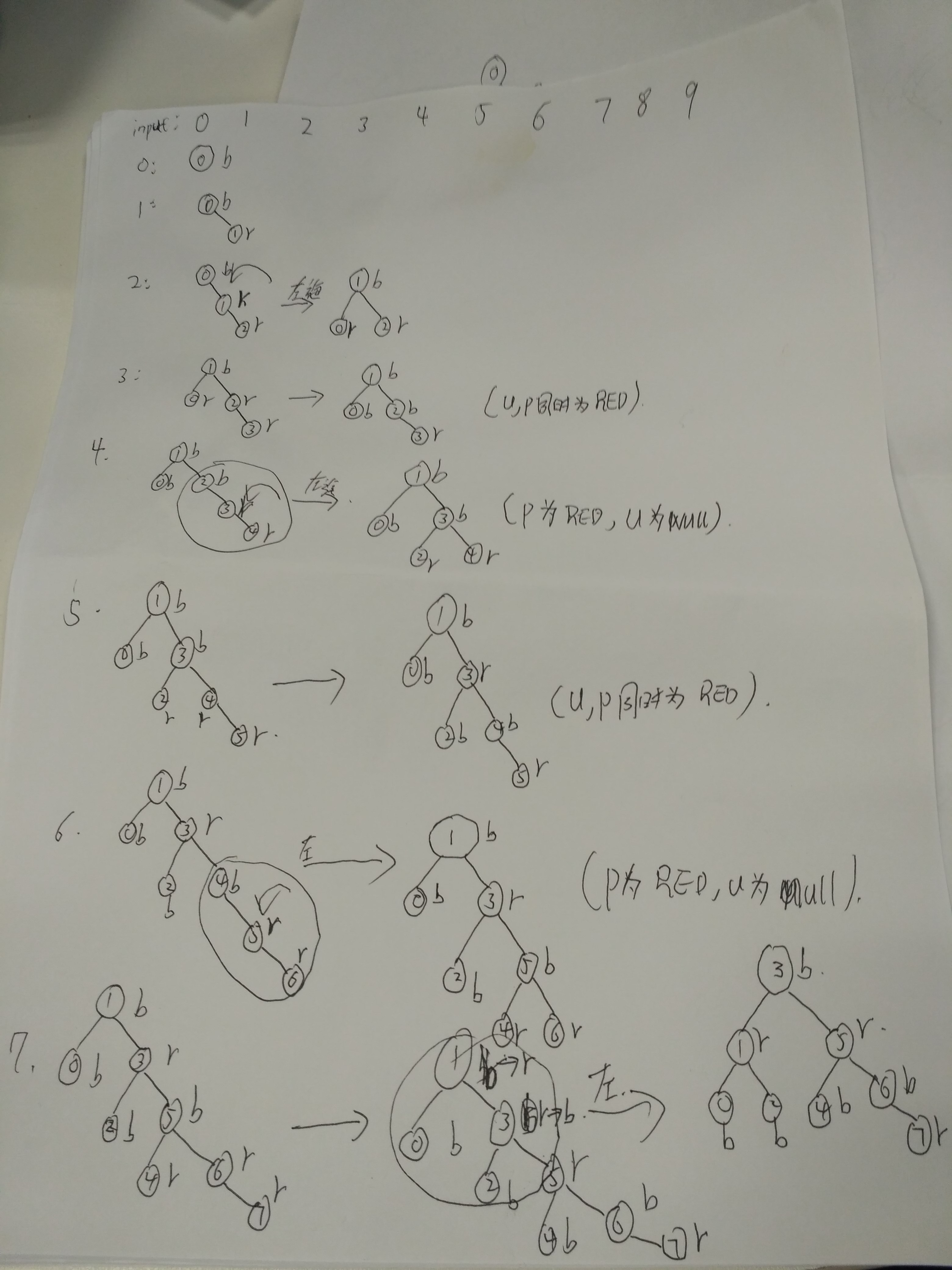![](http://images2017.cnblogs.com/blog/945140/201711/945140-20171114160902265-208312706.jpg)

          g.setColor(RED);
          node = g;
        } else {
          if (node == p.left) {
            rotateRight(p);
            Node tmp = p;
            p = node;
            node = tmp;
          }
          //當node 爲左孩子的時候
          p.color = BLACK;
          g.color = RED;
          rotateLeft(g);
        }
      }
    }
    //知足狀況1,實際上增長黑色節點高度一定時從這裏修改的,由於下面爲了保持性質5黑色節點高度
    // 不會增長,可是當新增節點最後致使根節點變爲了紅色,此時就會增長紅黑樹黑色節點高度.
    mroot.setColor(BLACK);
  }

左旋及右旋的代碼:

void rotateLeft(Node data) {
    Node temp = data.right;
    data.right = temp.left;
    if (data.right != null) {
      data.right.parent = data;
    }
    temp.parent = data.parent;
    if (data.parent == null) {
      mroot = temp;
    } else if (data.parent.left == data) {
      temp.parent.left = temp;
    } else {
      temp.parent.right = temp;
    }
    temp.left = data;
    data.parent = temp;
  }

  void rotateRight(Node data) {
    Node temp = data.left;
    data.left = temp.right;
    if (data.left != null) {
      data.left.parent = data;
    }
    //交換父節點
    if (data.parent == null) {
      mroot = temp;
    } else if (data.parent.left == data) {
      data.parent.left = temp;
    } else {
      data.parent.right = temp;
    }
    temp.parent = data.parent;

    temp.right = data;
    data.parent = temp;
  }

具體演化過程見我手畫的圖

1. 求p節點後繼節點:分爲2種狀況
   • p節點有右子樹--則其後繼節點爲其右子樹的最小節點(這個會在節點刪除的時候被調用)
   • p節點沒有右子樹--分爲兩種狀況
     • p節點的父節點及其祖父節點依次循環大於其父節點,即(p.parent.key>p.parent.parent.key),此種狀況致使p沒有後繼節點,由於p是最大的那個節點
     • p.parent=p.parent.parent,依次找到其父節點們第一個爲左子樹的狀況,則此祖父節點爲p的後繼節點.

Node successor(Node data) {
       if (data == null) {
         return null;
       }
       //後繼節點是右節點爲根的整棵樹上的最小節點
       else if (data.right != null) {
         return findMinNode(data.right);
       }
       //若是沒有右節點,則必爲其第一顆爲左子樹的祖父(包括父親)節點(由於其祖父類節點若爲右子樹,
       // 一定小於其前一個祖父類節點,一次類推,須要第一顆左子樹祖父類節點,若一直到頭沒有,則說明
       // 刪除的是整個樹的最大節點,故後繼節點爲null)
       else {
         Node s = data.parent;
         Node tmp = data;
         while (s != null && tmp == s.right) {
           tmp = s;
           s = s.parent;
         }
         return s;
       }
     }
   Node findMinNode(Node root) {
       if (root == null) {
         return null;
       } else {
         Node min = root;
         while (min.left != null) {
           min = min.left;
         }
         return min;
       }
     }

1. 刪除節點-刪除節點分爲4大類:
   • 被刪除節點只有左子樹--則用其右孩子代替其位置
   • 被刪除節點只有左孩子--則用其左孩子代替其位置
   • 被刪除節點既有左孩子又有右孩子--則把其後繼節點的值copy過來,其後繼節點一定沒有左孩子,並把後繼節點代替其爲被刪除節點(值已經被copy了,因此能夠刪除後繼節點),其後繼節點或者只有左孩子,變爲狀況2,或者沒有孩子,變爲狀況4
   • 被刪除節點沒有孩子--分爲兩大類
     • 被刪除節點爲根節點則此樹被所有刪除
     • 被刪除節點爲葉子節點則刪除便可.

String remove(int key) {
       Node node = getNode(key);
       if (node == null) {
         return null;
       }
       String oldValue = node.value;
       remove(node);
   //    deleteNode(node);
       return oldValue;
     }

code

private void remove(Node node) {
       Node p = node;
       //將被刪除的節點改成刪除其後繼節點,並把後繼節點的值copy過來
       if (node.left != null && node.right != null) {
         Node s = successor(node);
         p.key = s.key;
         p.value = s.value;
         p = s;
       }
       //replacement有4中狀況得來,(1)只有左孩子(2)只有右孩子
       //(3)左孩子右孩子都不爲空時其後繼節點的左孩子必爲空.
       //(4)爲空,又分爲兩種狀況:一是被刪除的節點是惟一一個節點,二是被刪除的節點是葉子節點.
       Node replacement = (p.left == null ? p.right : p.left);
       if (replacement != null) {
         replacement.parent = p.parent;
         //刪除的是跟節點
         if (p.parent == null) {
           mroot = replacement;
         } else if (p.parent.left == p) {
           p.parent.left = replacement;
         } else {
           p.parent.right = replacement;
         }
         p.left = p.right = p.parent = null;
         if (p.color == BLACK) {
           //修復可能產生兩個紅色節點
           fixDeletionRBT(p);
         }
       }
       //單獨的一個節點
       else if (p.parent == null) {
         mroot = null;
       }
       //葉子節點
       else {
         if (p.parent.left == p) {
           p.parent.left = null;
         } else {
           p.parent.right = null;
         }
         p.parent = null;
         if (p.color == BLACK) {
           //修復葉子節點可能爲紅色
           fixDeletionRBT(p);
         }
       }
     }

測試:懶得沒有寫全,基本上人工看了一下.

@Test
     public void remove() throws Exception {
       Node node8 = new Node(8, "8");
       Node node4 = new Node(4, "4");
       Node node12 = new Node(12, "12");
       Node node2 = new Node(2, "2");
       Node node6 = new Node(6, "6");
       Node node10 = new Node(10, "10");
       Node node14 = new Node(14, "14");
       Node node1 = new Node(1, "1");
       Node node3 = new Node(3, "3");
       Node node5 = new Node(5, "5");
       Node node7 = new Node(7, "7");
       Node node9 = new Node(9, "9");
       Node node11 = new Node(11, "11");
       Node node13 = new Node(13, "13");
       Node node15 = new Node(15, "15");
       keyStore.insert(node8);
       keyStore.insert(node4);
       keyStore.insert(node12);
       keyStore.insert(node2);
       keyStore.insert(node6);
       keyStore.insert(node10);
       keyStore.insert(node14);
       keyStore.insert(node1);
       keyStore.insert(node3);
       keyStore.insert(node5);
       keyStore.insert(node7);
       keyStore.insert(node9);
       keyStore.insert(node11);
       keyStore.insert(node13);
       keyStore.insert(node15);
       //測試刪除根節點-----至關於既有left,又有right
       keyStore.levelScan();
       keyStore.remove(8);
       System.out.println("刪除節點之後");
       keyStore.levelScan();
       //測試刪除節點只有右子樹
       keyStore.remove(10);
       System.out.println("刪除節點之後");
       keyStore.levelScan();
       //測試刪除葉子節點
       keyStore.remove(15);
       System.out.println("刪除節點之後");
       keyStore.levelScan();
       //測試刪除節點只有左子樹
       keyStore.remove(14);
       System.out.println("刪除節點之後");
       keyStore.levelScan();
       //測試刪除葉子節點
       keyStore.remove(3);
       keyStore.levelScan();
       keyStore.removeAll();
       keyStore.insert(new Node(1,"1"));
       //刪除單節點
       keyStore.remove(1);
       keyStore.levelScan();
     }

完整版見個人另外一個博客.這個MD有毒,我用起來不舒服!

RBT