GHM論文筆記（CVPR2019）

[toc]

做者要解決的問題

仍然是one-stage中的一個經典問題，正負、難易樣本不均衡。由於anchor的緣由，pos : neg>= 1 : 70。負樣本大多比較簡單，因此也致使了難易樣本的問題。

Focal loss(CVPR2017)

Focal loss的解決方案

傳統的交叉熵損失函數： $$ L_{CE} = -[p^(log(p) + (1-p^)log(1-p)] $$ $p^*={0, 1}$爲真實標籤，$p \in (0, 1)$爲網絡的預測機率。能夠看到，傳統的交叉熵損失函數平等的看待正負樣本。 Focal loss $$ L = -[\alpha p^\gamma p^log(p) + (1-\alpha)(1-p)^\gamma (1-p^)log(1-p)] $$ 能夠看到Focal loss引入了兩個超參數$\alpha, \gamma$，$\alpha$用來平衡正負樣本，$\gamma$用來平衡難易樣本。簡單分析一下，加號的左側是正樣本的損失，右側是負樣本的損失。經過乘上不一樣的係數$(\alpha, 1-\alpha)$，來平衡正負樣本。對於簡單樣本，其loss較小，機率值更接近真實標籤，這樣機率的$\gamma$次方越小，相反地，難樣本的就會變大，使難樣本的損失上升，使網絡關注難樣本。

Focal loss的不足

雖然Focal loss這篇論文也在必定程度上解決了正負樣本不均衡的問題，可是Focal loss引入了兩個超參數，調參費勁，且只能應用到box分類上，沒法解決迴歸的問題。

設計思路

梯度與樣本的關係

做者觀察到難易樣本的分佈與梯度有着以下的關係，能夠看到，梯度較小時（簡單樣本），樣本數量很是多，梯度適中時，樣本較少。另外值得注意的一點是，梯度在1左右的樣本數量仍是很多的。做者將這些樣本視爲異常值，解決特別難的樣本會致使其餘的樣本準確率降低。

<div align=center><img src="https://img2018.cnblogs.com/blog/1809294/201912/1809294-20191202201513553-1553490396.png"></div> 針對以上發現，做者採用梯度分佈（梯度附近的樣本數）來處理難易樣本不平衡的問題。簡單思路就是梯度小的樣本數比較大，那就給他們乘上一個小系數，梯度大的樣本少乘以一個大的係數。不過這個係數不是靠本身調的，而是根據樣本的梯度分佈來肯定的。 ### 梯度分佈計算方法：將0-1的梯度切bin，計算每一個bin內落入的樣本數量。 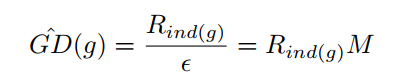 其中$\epsilon$是每一個bin的寬度，$M$是$\epsilon$的倒數，表示將0-1切分紅多少個bin，$R_{ind(g)}$表示每一個bin內落入的樣本數，計算方法以下：

$$ R_{ind(g)} = \sum_{k=1}^{N} \delta(g_k,g) \quad \delta(g_k,g) = \begin{cases} 1 \quad if \quad g-\frac{\epsilon}{2} <= g_k <= g+\frac{\epsilon}{2}\ 0 \quad otherwise \end{cases} $$

$$ \beta_i = \frac{N}{GD(g_i)} $$ $g$是某點的梯度模，能夠理解爲以這一點建立一個bin，$g_k$是樣本的梯度模，N是樣本總數。 從上面式子能夠看到，梯度分佈越大，係數越小。

梯度模計算方法

具體的在二分類中,損失函數爲上面提到的交叉熵函數 $$ L_{CE} = -[p^(log(p) + (1-p^)log(1-p)] \ p=sigmoid(x) $$ 對x的梯度 $$ \begin{aligned}\frac{\partial L_{CE}}{\partial x} &= \frac{\partial L_{CE}}{\partial p} \times \frac{\partial p}{\partial x}\&= (-\frac{p^}{p} + \frac{1-p^}{1-p}) \times p(1-p)\&= p-p^\end{aligned} $$ 定義梯度模$g = |p-p^|$

改進

GHM－C損失函數

由此，做者提出分類的損失函數GHM-C $$ L_{GHM-C} = \frac{1}{N}\sum\beta_i L_{CE}(p_i, p_{i}^{*}) $$

<div align=center><img src="https://img2018.cnblogs.com/blog/1809294/201912/1809294-20191202201513553-1553490396.png"></div> 仍是以這個圖爲例，在梯度較小時，樣本數較大，梯度分佈$GD(g)$較大，則係數較小，損失較小，這樣就有效的減小了大量簡單樣本的做用。反之亦然。一樣能夠分析出特別難的樣本也被抑制了。這一點也是做者但願看到的。 下面這張圖的橫座標表明原先的梯度分佈，縱座標表明處理後的梯度分佈。對比未經任何處理的CE曲線，在0附近的梯度，GHM-C處理後梯度被減少了，0.5左右的樣本梯度被放大了，尤爲值得一提的是，對於前面提到的異常樣本，梯度一樣被抑制了。對比Focal loss曲線，明顯能夠看出GHM-C更加優秀。 <div align=center><img src="https://img2018.cnblogs.com/blog/1809294/201912/1809294-20191202201722361-1423552019.png"></div> #### GHM－R損失函數 按理說像以前同樣求下梯度分佈就行了，不過這裏有一個問題。 對於邊框迴歸的傳統損失函數smooth_L1 <div align=center><img src="https://img2018.cnblogs.com/blog/1809294/201912/1809294-20191202202014607-517726503.png"></div> 求梯度模 $d= t_i - t_i^*$ <div align=center><img src="https://img2018.cnblogs.com/blog/1809294/201912/1809294-20191202202051866-2021027845.png"></div> 能夠看到，當$d>\delta$時，梯度模橫爲1，沒法衡量樣本的難易程度。因此做者這裏改了一下 <div align=center><img src="https://img2018.cnblogs.com/blog/1809294/201912/1809294-20191202202142141-374861646.png"></div> d比較小的時候，相似於$L_2$，d較大時候相似$L_2$，和$SL_1$相似。最終的損失函數以下： <div align=center><img src="https://img2018.cnblogs.com/blog/1809294/201912/1809294-20191202202350370-803095327.png"></div> 注意一點：迴歸的損失函數是隻計算正樣本的。 ## 最終結果 COCO數據集上的比較 <div align=center><img src="https://img2018.cnblogs.com/blog/1809294/201912/1809294-20191202202428979-898801669.png"></div> 只有GHM-C的比較 <div align=center><img src="https://img2018.cnblogs.com/blog/1809294/201912/1809294-20191202202450943-1297614676.png"></div> 只有GHM-R的比較 <div align=center><img src="https://img2018.cnblogs.com/blog/1809294/201912/1809294-20191202202453290-1446090138.png"></div>