[ML]熵、KL散度、信息增益、互信息-學習筆記

熵

Entrophy:

sum([p*log(1/p) for each p])

p:      1次實驗的， x的發生的次數的指望是 p
1/p :   x發生1次， 指望要作的試驗次數是 1/p

Example

1. 硬幣：

T: 1/2
H: 1/2

由霍夫曼編碼，編碼的指望長度最小是 1 bit

用熵來解釋, T發生一次， 指望要作的試驗次數是 2

log(2) = 1
1/2 * log(2) = 1/2

H也同樣，因而就有：

1/2 + 1/2 = 1 (bit)

1. 摸球

4個球 1個紅球 2個綠球 1個黑球

紅球的機率 1/4
綠球 2/4=1/2
黑球 1/4

1/4 * log(4) = 1/2
1/2 * 1 = 1/2
1/4 * 2 = 1/2

1/2 + 1/2 + 1/2 = 3/2 (bit)
指望的編碼長度是 3/2， 一樣和霍夫曼編碼結果同樣。

a, b 出現機率分別是 1/2， 熵是1， 所須要的比特位是1

1/p : 平均2個字符中會獲得一個 a log(1/p):1個bit所表明的狀況中平均能獲得一個a
1/(1-p): 平均2個字符會獲得一個 b log(1/(1-p)):1個bit所表明的狀況中平均能獲得一個b

須要bit的機率 = 
    出現一個a的機率 * 出現一個a的狀況下須要多少bit +
    出現一個b的機率 * 出現一個b的狀況下須要多少bit

相對熵 (KL散度)

wiki

KL散度是兩個機率分佈P和Q差異的非對稱性的度量。 KL散度是用來 度量使用基於Q的編碼來編碼來自P的樣本平均所需的額外的比特個數。 典型狀況下，P表示數據的真實分佈，Q表示數據的理論分佈，模型分佈，或P的近似分佈。

D(Q||P)=∑Q(x)[log(1/P(x))] - ∑Q(x)[log[1/Q(x)]]
         =∑Q(x)log[Q(x)/P(x)]


∑Q(x)[log(1/P(x))] 表示使用原來的編碼方式獲得的比特數的指望

log(1/P(x)) 表示使用原來的編碼方式，x出現1次的指望編碼長度
Q(x) 表示如今x出現的機率

因爲-log(u)是凸函數，所以有下面的不等式

DKL(Q||P) = -∑x∈XQ(x)log[P(x)/Q(x)] = E[-logP(x)/Q(x)] ≥ -logE[P(x)/Q(x)] = -log∑x∈XQ(x)P(x)/Q(x) = 0

即KL-divergence始終是大於等於0的。當且僅當兩分佈相同時，KL-divergence等於0。

舉一個實際的例子吧：好比有四個類別，一個方法A獲得四個類別的機率分別是0.1,0.2,0.3,0.4。另外一種方法B（或者說是事實狀況）是獲得四個類別的機率分別是0.4,0.3,0.2,0.1,那麼這兩個分佈的KL-Distance(A,B)=0.1*log(0.1/0.4)+0.2*log(0.2/0.3)+0.3*log(0.3/0.2)+0.4*log(0.4/0.1)

這個裏面有正的，有負的，能夠證實KL-Distance()>=0.
從上面能夠看出， KL散度是不對稱的。即KL-Distance(A,B)!=KL-Distance(B,A)
KL散度是不對稱的，固然，若是但願把它變對稱，

Ds(p1, p2) = [D(p1, p2) + D(p2, p1)] / 2

KL散度是兩個機率分佈P和Q差異的非對稱性的度量。 KL散度是用來 度量使用基於Q的編碼來編碼來自P的樣本平均所需的額外的比特個數。 典型狀況下，P表示數據的真實分佈，Q表示數據的理論分佈，模型分佈，或P的近似分佈。

條件熵

wiki

條件熵是信息論中信息熵的一種度量，它表示若是已經徹底知道第二個隨機變量 X 的前提下，隨機變量 Y 的信息熵還有多少。也就是 基於 X 的 Y 的信息熵，用 H(Y|X) 表示。同其它的信息熵同樣，條件熵也用比特、奈特等信息單位表示。

具體有針對一個肯定的Xj 的條件熵， 若是是針對一個隨機變量而言， 條件熵是針對全部Xj的條件熵的指望

聯合熵

wiki

P(x,y) 是聯合機率

信息

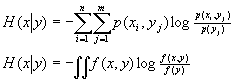
由對數性質和全機率公式

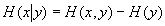
信息是經過熵與條件熵的差計量的

擲一次骰子，因爲六種結局（點）的出現機率相等，因此結局的不肯定程度（熵）爲log6 ，若是告訴你擲骰子的結局是單數或者雙數，這顯然是一個信息。這個信息消除了咱們的一些不肯定性。把消除的不肯定性稱爲信息顯然是穩當的。

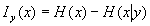
若是令公式中的y=x，H(x∣y)變成了H(x∣x)，其含義固然是x已知時x的條件熵，但是x 已知時它本身固然沒有不肯定性了。因此H(x∣x)=0 。把它帶入信息公式，獲得

也就是說x 值已知時所帶來的信息剛好等於原來的不肯定性。或者說x。這正是在一些場合下把熵直接稱爲信息的緣由。遺憾的是有些人沒有理解這個認識過程，而引出了信息是熵或者信息是負的熵的概念混亂。

信息增益

熵下降的程度
信息是經過熵與條件熵的差計量的

互信息

http://zh.wikipedia.org/wiki/%E4%BA%92%E4%BF%A1%E6%81%AF

互信息（Mutual Information）是一有用的信息度量，它是指兩個事件集合之間的相關性。兩個事件X和Y的互信息定義爲：

baike:
通常而言，信道中老是存在着噪聲和干擾，信源發出消息x，經過信道後信宿只可能收到因爲干擾做用引發的某種變形的y。信宿收到y後推測信源發出x的機率，這一過程可由後驗機率p(x|y)來描述。相應地，信源發出x的機率p(x)稱爲先驗機率。咱們定義x的後驗機率與先驗機率比值的對數爲y對x的互信息量，也稱交互信息量（簡稱互信息）。

其意義：因爲事件A發生與事件B發生相關聯而提供的信息量。

該方法經過計算詞條和類別的互信息，詞條和類別的互信息越大，詞條越能表明該種類別。其中詞條和類別的互信息經過公式，

MI(T,C) = log( P(T|C)/P(T) )

MI(T,C) = H(C)-H(C|T)

熵 - 條件熵 ， 這個和信息增益也有關係， 具體見 綜合 部分.

其中P(T｜C)是詞條T在類別C中出現的機率，P(T)是詞條T在整個訓練集中出現的機率。

直觀理解， 若是 T在整個訓練集中出現的機率並不高，可是在類別C中出現的機率卻很高， 那麼就能夠知道T能夠很大程度上表明這個C, 分子相似於tf（可是包含了文檔長度的考慮）, 分母有點相似於IDF（可是又包含了各個文檔中出現的term的個數，而不僅是出沒出現）。

用互信息的方法，在某個類別C中的出現機率高，而在其它類別中的出現機率低的詞條T，將得到較高的詞條和類別互信息，也就可能被選取爲類別C的特徵。

互信息是term的存在與否能給類別c的正確判斷帶來的信息量。

詞條和類別的互信息體現了詞條和類別的相關程度，互信息越大，詞條和類別的相關程度也越大。獲得詞條和類別之間的相關程度後，選取必定比例的，排名靠前的詞條做爲最能表明此種類別的特徵。

自信息

http://zh.wikipedia.org/wiki/%E8%87%AA%E4%BF%A1%E6%81%AF

自信息（英語：self-information），又譯爲信息本體，由克勞德·香農提出，用來衡量單一事件發生時所包含的信息量多寡。它的單位是bit,或是nats。

特徵選擇

決策樹：
特徵t能產生的信息增益 = 熵 - t對應的條件熵

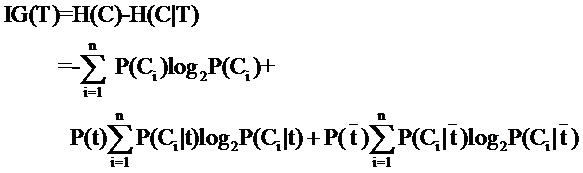
Xj -> X, 這裏j只有兩種取值， 有 或者 沒有， 也就對應了決策樹的兩個分叉。

選擇信息增益最大的特徵。

實際中特徵t多是一個連續值，咱們須要選一個閾值，大於閾值的就等同於t出現， 小於閾值的就等同於t不出現，這個閾值也須要遍歷全部的樣本集中t的取值來肯定。 一樣仍是兩個分叉。 假設有n個特徵，m個樣本（最壞在每一個特徵處有m個值， 這樣尋找一次最大的信息增益的複雜度是 O(mn) 仍是挺大的）

若是有一個樣本集是這樣

f1 f2 f3
c1   1  0  1
c2   0  1  0
c3   1  1  0

能夠算c1 c2之間的類似度， 一樣也能夠算 f1, f2之間的類似度， 行和列而已, 實際中 c1 c2 c3不可能就一個樣本

f1 f2 f3
c1   1  0  1
c1   1  1  1
c2   0  1  0
c2   1  1  0
c3   1  1  0

這時候直接算列的類似度就很差算了， 用互信息就能夠，互信息就像是把類別做爲一個doc， 特徵做爲term， 的tf-idf模型， 好比f3就很能表明c1, 一樣， 用信息增益也能夠算。

綜合

Wiki : Information gain in decision trees

In information theory and machine learning, information gain is a synonym for Kullback–Leibler divergence. However, in the context of decision trees, the term is sometimes used synonymously with mutual information, which is the expectation value of the Kullback–Leibler divergence of a conditional probability distribution.

In particular, the information gain about a random variable X obtained from an observation that a random variable A takes the value A=a is the Kullback-Leibler divergence DKL(p(x | a) || p(x | I)) of the prior distribution p(x | I) for x from the posterior distribution p(x | a) for x given a.

證實：

http://www.cnblogs.com/xiedan/archive/2010/04/03/1703722.html
http://blog.sohu.com/people/f21996355!f/123258006.html

http://blog.sina.com.cn/s/blog_4d1f33470100sjuf.html 這篇文章提到互信息能夠和 tf-idf 同樣做爲文檔的關鍵詞的權值