關於隨機數的前世此生

提起隨機數，你們必定都不陌生。不管是在計算機科學領域，仍是現實生活中，隨機數的做用都不可小覷。

但隨機數到底是怎麼一會事？它的做用是什麼？它有事如何產生的？

本文會着重談計算機的隨機數以及產生算法，偏理論的只是會放到另外一篇博客上[隨機數那些事](https://www.luogu.org/blog/muxii/sui-ji-shuo-wei-wan-cheng-post)

# 隨機數定義及其性質

想要討論隨機數，首先應該明確一下隨機數的定義。畢竟這個東西比較虛，並不像算法那樣明確。在各大網上也沒有給出很好的定義。

那...就不死摳定義了。

隨機數通常來講符合下面這幾個性質。

>1. 它產生時後面那個數與前面的毫無關係

>1. 給定樣本的一部分和隨機算法，沒法推出樣本的剩餘部分

>1. 其隨機樣本不可重現

另外還要說一下統計學僞隨機數概念，**劃重點**

##### 統計學僞隨機性。統計學僞隨機性指的是在給定的隨機比特流樣本中，1的數量大體等於0的數量，同理，「10」「01」「00」「11」四者數量大體相等。相似的標準被稱爲統計學隨機性。知足這類要求的數字在人類「一眼看上去」是隨機的。（摘自百度詞條）

實際上這也是在計算機中對僞隨機數優劣的概念。

continue->

# 僞隨機數

僞隨機數，也就是咱們c++中經常使用的隨機數。爲何說它是「僞」隨機呢？其實只要稍微詳細的瞭解過c++ rand函數的人應該都能懂得這一點。

由於計算機自己並不可以產生和隨機數，只能經過產生一組循環節很長的數來「僞造」隨機。

c++的rand函數實際上只是根據你提供的種子計算出來的一組循環節很長的數。只要兩次提供的種子是同樣的，那麼rand函數提供的隨機數也是同樣的。

可能有好奇的小夥伴就要問了，你說循環節很長，那到底長到什麼程度呢？

通過不懈的努力，筆者成功弄到了rand()函數在LINUX系統下的實現：

```
static unsigned long next = 1;

/* RAND_MAX assumed to be 32767 */
int myrand(void) {
next = next * 1103515245 + 12345;
return((unsigned)(next/65536) % 32768);
}

void mysrand(unsigned seed) {
next = seed;
}
```
（ 該代碼摘自CSDN [原文連接](https://blog.csdn.net/Cashey1991/article/details/45042291)）

經過這個算法咱們能夠推知，rand函數的循環節應該是在32768（2的15次方）之內。

（ 因此我白測試了是嗎 ）

作這些測試實際上就是想說，在計算機方面。目前來講，若是不借助外部幫助，是沒法達到真隨機的。

# 計算機的隨機數

計算機隨機數的產生，我在講僞隨機時已經~~水過~~作過介紹了，也就很少說。

你覺得我會幫忙把前面的代碼拷過來嗎？想太多了，本身翻頁去。

（ 原本想放點圖可能能夠增長可讀性，但好像放不了什麼... ）

這裏我主要想講的是關於計算機在沒有外界幫助下爲何不能產生真隨機數。

真隨機數的產生應該是與以前的數是沒有任何關聯的（ 論證過 ），那麼在計算機中想對應的就是產生隨機數的函數應該不須要調用任何參數（ 由於一旦調用了的參數，那麼這個隨機數的產生就會與參數相關 ）那麼對於計算機來講，如何不調用任何參數而且產生不一樣的數呢？

這個...好像作不到。

這個換一個思惟來解釋好一點。由於計算機是一個絕對理智的存在，也就是說，計算機的一切行爲都是可預測可推導的。而這偏偏違背了咱們隨機數標準中的第二條，即不可推斷。對於計算機的任何程序，若是使用徹底相同的參數來調用，它所輸出的結果必定是徹底同樣的

農夫山泉不生產水，他們只是大天然的搬運工


計算機不生產數據，它只是數據的加工廠。


# 真隨機數生成

不是重點，知道了就好。

真隨機數生成器是一種經過物理過程而不是計算機程序來生成隨機數字的設備。

這樣的設備一般是基於一些能生成低等級、統計學隨機的「噪聲」信號的微觀現象，如熱力學噪聲、光電效應和量子現象。這些物理過程在理論上是徹底不可預測的，而且已經獲得了實驗的證明。硬件隨機數生成器一般由換能器、放大器和模擬數字轉換器組成。其中換能器用來將物理過程當中的某些效果轉換爲電信號，放大器及其電路用來將隨機擾動的振幅放大到宏觀級別，而模擬數字轉換器則用來將輸出變成數字，一般是二進制的零和一。經過重複採樣這些隨機的信號，一系列的隨機數得以生成。

（摘自百度詞條[原文連接](https://baike.baidu.com/item/%E7%9C%9F%E9%9A%8F%E6%9C%BA%E6%95%B0%E7%94%9F%E6%88%90%E5%99%A8/13023188?fr=aladdin)）

# 隨機數在OI中的常見應用

首先是用於檢驗程序。

估計這是大部分OIer的用法，拿一個隨機數生成器去驗證程序的速度,以及是否會RE（ 正確率是測不了的，畢竟本身手推答案比較慢 ）。

而後的話是某些算法的須要

這裏由於算法太多，筆者也就大概介紹一下：

>1. 你們熟悉的平衡樹treap，它是經過生成隨機權值引導進行旋轉操做來使樹接近平衡。

>2. 相對常見的模擬退火就是隨機算法的一個極致實現。它經過徹底隨機的操做變換解，使其不斷接近正解。也是你們在OI中最多的用法。

>3. 可能你們相對陌生的遺傳算法中也有隨機數的體現。主要表如今交叉和變異兩方面上。

>4. 可能你們聽都沒通說過的Pollard_Rho算法，就是超大數的分解質因數。由於數字過大沒法用O（N）的算法。此時咱們就經過隨機數去「猜」質因數：不斷生成隨機值，判斷是否出現二者之差爲因子。（由於二者差爲指定值的出現機率會比一個個猜大一倍），而後不斷遞歸隨機到的那個因子和那個數初一因子的另外一半，直到找到質因子。具體算法比較複雜。有機會單獨寫一篇講。[模板題傳送門](https://www.luogu.org/problem/P4718)

>5. 而後與遺傳算法相似的粒子羣算法，隨機主要出如今單個粒子的更新上。

>6. 蟻羣算法有用到，但由於過於冷門，就很少作介紹了。

（ 感受隨機數好像也就這麼點用，在密碼學統計學中用的比較多 ）

# 隨機數優劣斷定

在講隨機數算法以前，應該先講講隨機數優劣的斷定。

畢竟只有清除了隨機數的優劣，咱們才能說如何生成優質隨機數。

在這裏咱們就要用到前面說的統計學僞隨機性：

統計學僞隨機性。統計學僞隨機性指的是在給定的隨機比特流樣本中，1的數量大體等於0的數量，同理，「10」「01」「00」「11」四者數量大體相等。相似的標準被稱爲統計學隨機性。知足這類要求的數字在人類「一眼看上去」是隨機的。（我幫忙搬下來了）

結合計算機隨機數的特性，咱們可以得出如下三項判斷隨機數優劣的性質：

>1. 隨機程度，即隨機算法是否足夠複雜，隨機數之間會不會存在明顯聯繫。

>2. 分佈範圍，便是否存在隨機數在分佈區域內大量出現偏大偏小的現象。分佈是否足夠平均。

>3. 循環長度，便是否會在大量調用時很快地出現循環的狀況。

有了這些評判規則，咱們就比較好學習優質隨機數的生成。

# 如何生成優質隨機數

終於到了塞實貨時間。

~~水不動了~~

這裏前三個我講一下在rand函數調用基礎上本身作一點小操做來產生三種不一樣特性的隨機數。

第四個專題講MT19337算法（**重點，絕對的重點**），也就是目前優質隨機數生成的廣泛算法。

### 來回擺動式

這種隨機數主要是針對退火算法之類的須要用隨機數來修正答案的。

既然是修正答案，那麼咱們但願最好是來回擺動，一正一負的。

這種隨機數的特色即是經過一部分人工處理，將本來的rand函數產生的隨機數變成正負交替的。

```cpp
int f = 3000 ;
int change = 0.999 ; // f和change是用來控制隨機數幅度不斷變小的
int con = -1 ;
int g = 1 ; // 控制正負交替
int newrand ( ) {
f *= change ;
g *= con ;
int tmp = f * g * rand ( ) ;
return tmp ;
}
```

這種隨機數的產生引入了退火的思路，固然，你也能夠直接使用算法中現成的溫度來控制。

### 平均式

這種主要是用於平衡樹treap的，特色就是在保證單個數隨機的狀況下在總體上保證分佈比較平均。

實現原理也沒什麼好講的，上代碼就完事了。

```cpp
int p ; // 但願的分佈位置
int newrand ( ) {
int tmp = ( p + rand ( ) ) / 2 ; // 經過取於分佈位置的平均數，是產生的數更加靠近但願分佈
return tmp ;
}
```

### 屢次調用不重複式

固然，若是有人真的須要很是接近真隨機的數。也就是屢次運行程序也不會出現相同的狀況。那就須要用到必定的外部干擾了。

首先是clock函數，上文已經說過，一個程序在不斷調用期間。每一次的運行時間都會有細小的變化。咱們就能夠利用好這個變化。每次調用完後都重置一次隨機數種子。

還有一個可能你們都會忽視的方法。計算機自己的偏差。衆所周知，計算機在作浮點運算時是會產生精度損失的，那麼咱們也能夠利用這個特色輔助clock調整種子（畢竟程序調用時間相同其實可能性也不小，畢竟clock只精確到s/1000）。

```cpp
int count ;
int realrand ( ) {
count ++ ;
int t = clock ( ) + 1 ; // 使用當前時間
for ( int i = 1 ; i < 12121307 ; i ++ ) { // 降速（若是放到具體代碼裏面使用能夠將此參數調低）
t += rand ( ) ;
}
t += clock ( ) ; // 降速後擴大時間變化
t *= -1234 ;
srand ( t * count + rand ( ) ) ; // 重置隨機數種子
return rand ( ) ;
}
```

筆者通過大量實驗，發現該函數前三個數出現重複概率相對會比較大（7~9%）建議從第四個開始使用。

上面的代碼我並沒用用精度損失來隨機化，由於我發現同一個式子的進度損失值過小，以致於幾乎不會發生什麼改變，因此並無使用。

### 隨機數優劣度分析：

由於三個函數實際上都是在調用rand()函數，因此實際上他們的優質程度是與rand()函數相同的。記得我以前題的判斷隨機數優劣的標準嗎？

>1. 隨機程度，即隨機算法是否足夠複雜，隨機數之間會不會存在明顯聯繫。

>2. 分佈範圍，便是否存在隨機數在分佈區域內大量出現偏大偏小的現象。分佈是否足夠平均。

>3. 循環長度，便是否會在大量調用時很快地出現循環的狀況。

就是這個

咱們來逐條分析。

首先，隨機程度方面，雖然大家以前看過rand()函數代碼，可能清楚數字之間的關聯
。但在實際運用中，這個數字之間的關聯仍是基本能夠忽略的。因此在隨機程度方面，rand()函數仍是可以勉強經過的。

在平均分佈方面，單看代碼可能感受不出來。

那麼，筆者就作一個測試：

```cpp
#include<iostream>
#include<stdlib.h>
using namespace std ;
int data[1000] ;
int main ( ) {
for ( long long i = 1 ; i <= 100000000 ; i ++ ){
int tmp = rand ( ) % 100000 ; //生成一個100000之內的隨機數
data[ tmp / 10 ] ++ ; //統計出現次數
}
for ( int i = 1 ; i <= 100 ; i ++ ) {
cout << data[i] << endl ;
}
cout << " ok " << endl ;
return 0 ;
}
```

最後結果：


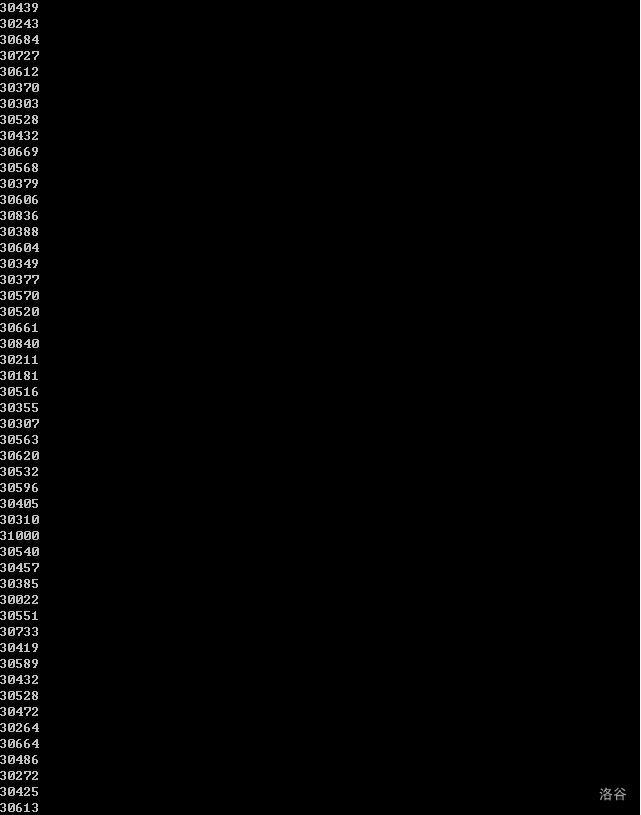
從中咱們能夠看到，這個分佈仍是很是平均的。

循環長度...

這個主要就是rand()函數的硬傷了，32768這個長度真的挺不夠用的。在須要大量調用rand()函數的算法中（好比退火），基本都會把rand()卡出循環。

那有沒有既優質又循環節長的算法呢？

# 梅森旋轉算法（MT19337）

**這個很重要，因此標題升了一級**

這個是目前產生優質僞隨機數的廣泛算法

在C++11，python等多種語言中都有使用# 旋轉算法簡介

梅森旋轉算法，也能夠寫做MT19937。是有由松本真和西村拓士在1997年開發的一種能快速產生優質隨機數的算法。

其實這個算法跟梅森沒有什麼關係，它之因此叫作是梅森旋轉算法是由於它的循環節是2^19937-1，這個叫作梅森素數。

這個算法之因此說是產生優質隨機數，是由於它在循環節特別長的狀況下（2^19337-1）還能保證平均分佈。

#### 可能有的同窗對這個循環節有點質疑。可能以爲2^19937-1有點短？

我在這裏大概給一個概念：

銀河系中的恆星數量級10^11

撒哈拉沙漠中的沙子數數量級是10^26

宇宙中目前可觀察的粒子數量級是10^87

**2^19937數量級是10^6001**

這個比較大概內心有數了吧

相差的已經不止是一個數量級了

同時他在623維中的分佈都十分的均勻（這個不用理解）

知道分佈平均就行了


（梅森鎮樓）

->continue

# 前置知識

分析這個算法的原理須要的前置知識在網上講的都比較繞，我在這裏就通俗的科普一下，主要是認識這幾個名詞。

（用詞不許確輕噴）

#### 線性反饋移位寄存器（LFSR）


這個，就當它是隨機數發生器就完事了，不要太去糾結定義。後面會講。

#### 本原多項式

簡單的說來就是無法化簡的多項式

好比 $y=x^4+x^2$ 就能夠化簡爲$( x^2 + 1) x ^ 2$

也是知道就好，不用過於追求定義

#### 級

計算機的一個二進制單位（0或1）就是一級

這個應該比較好理解

#### 反饋函數

這個應該是網上看別的博客最繞的知識點

簡單地理解成你要對這個寄存器幹什麼的一個函數就行了

（看到這裏應該還沒懵吧）

#### 異或

這個...

還要我科普嗎？

就是兩個數，若是都是0或都是1就輸出0，一個1一個0輸出1.

->continue

# 原理分析

這個旋轉算法其實是對一個19937級的二進制序列做變換。

首先咱們達成一個共識：

一個長度爲n的二進制序列，它的排列長度最長爲2^n。

固然這個也是理論上的，實際上可能由於某些操做不當，沒挺到2^n個就開始循環了。

那麼如何將這個序列的排列撐滿2^n個，就是這個旋轉算法的精髓。

**若是反饋函數的自己+1是一個本原多項式，那麼它的循環節達到最長，即2^n-1**

這個數學證實本文不做過多論述，有興趣者能夠本身查閱資料

我的感受單講知識點挺難懂的（筆者就是這麼被坑的）

咱們就拿一個4級的寄存器模擬一下：

咱們這裏使用的反饋函數是 y=x^4+x^2+x+1（這個不是本原多項式，只是拿來好理解）

這個式子中x^4,x^2,x的意思就是咱們每次對這個二進制序列的從後往前數第4位和第2位作異或運算 ，而後x的意思是咱們再拿結果和最後一位作異或運算。把最後的結果放到序列的開頭，整個序列後移一位，最後一位捨棄。


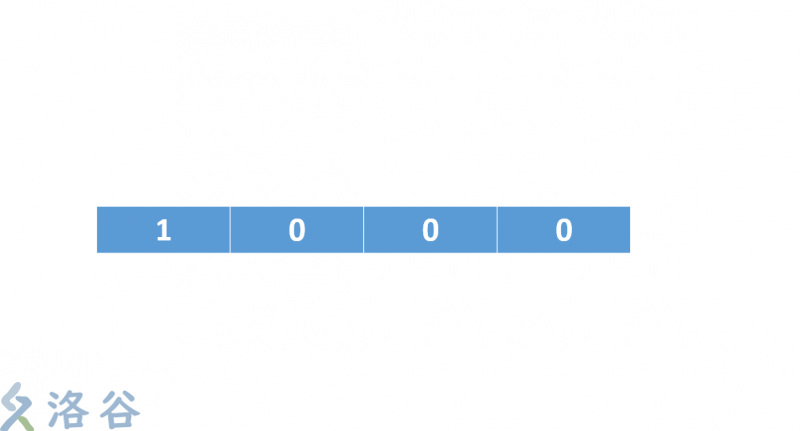
1. 初始數組 { 1 ， 0 ， 0 ， 0 } （爲何不是 0，0，0，0 大家能夠本身想一想，文章末尾揭曉）


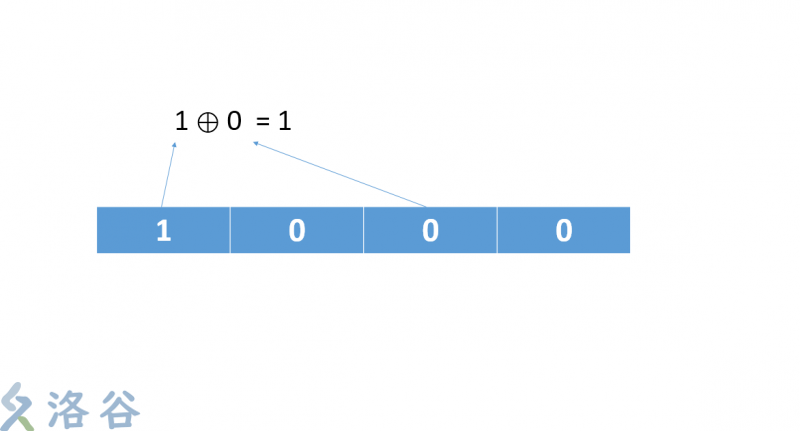
2. 將它的第四位和第二位抓出來作異或運算


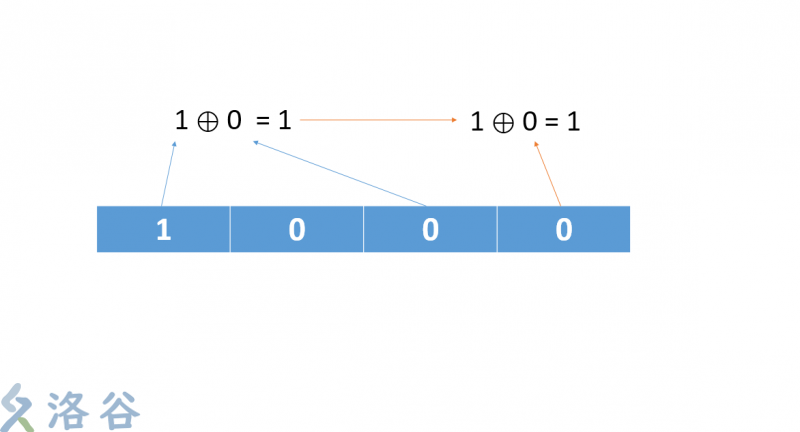
3. 把剛剛的運算結果和最後一位再作一次運算


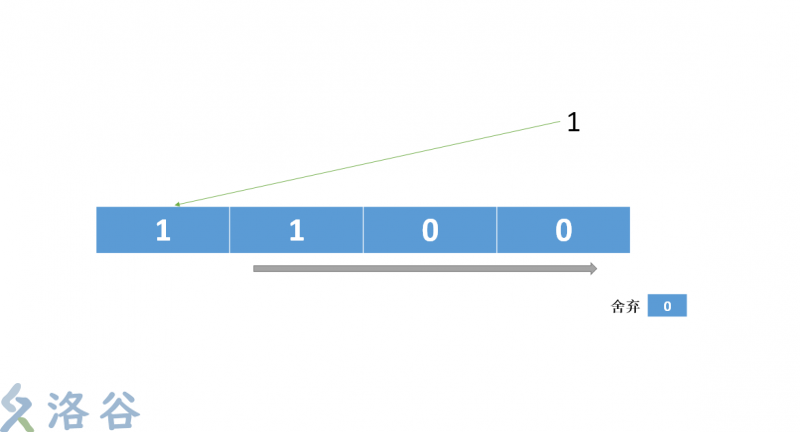
4. 把最後的運算結果放到第一位，序列後移。最後一位被無情的拋棄

這就是一次運算，而後這個算法就是不斷循環這幾步，從而不斷僞隨機改變這個序列。


上圖是一個網上找的一個4級寄存器的模擬過程

你們能夠推一下，它所使用的反饋函數（y=x^4+x+1）

由於這個是本原多項式

因此他最後的循環節是2^4-1=15

運算結果以下：


（圖片摘自[原文連接](https://www.cnblogs.com/mengfanrong/p/3840765.html)）

你們能夠看到這個運算結果包含到了2^4-1~1中的全部數字，而且沒有循環。

同時擁有很好的隨機性。

可能又有人有疑問了：

這個運算結果明明能看出規律啊，我不是看到了不少1的平行四邊形嗎？

醒醒

這是二進制數。

若是你把它轉化成數字。

8 12 14 15 7 11 ...

能看出規律？

#### 關於旋轉

可能有人到這裏還沒看出「旋轉」在哪裏。

由於咱們每次計算出來的結果會放在開頭，序列後移一位。看起來就像數組在向後旋轉...

（原本想作gif的，後來不知道怎麼作出旋轉）

你們自行腦補


->continue

### 算法評價

1.隨機程度：

這個應該不用說了，認真看這個原理的都應該清楚它的隨機程度比rand（）~~不知道高到哪裏去了~~。若是說rand（）還可以用公式表達的話，這個19337已經沒法經過算式表達了。

2.分佈範圍：

這裏筆者~~比較懶~~就不作證實了。有興趣的能夠拿上面的代碼自行檢測。

3.循環長度：

其實這點我能夠直接跳過的。19337算法最不慌的就是循環長度。2^19337的循環長度根本不需任何算法。畢竟人家這個算法的循環長度是與空間大小成指數級關係的……

# 代碼實現

（筆者很懶，直接搬[原代碼出處](http://www.it610.com/article/1902097.htm)的代碼）

```cpp
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <time.h>

using namespace std;

bool isInit;
int index;
int MT[624]; //624 * 32 - 31 = 19937

隨機種子
void srand(int seed)
{
index = 0;
isInit = 1;
MT[0] = seed;
for(int i=1; i<624; i++)
{
int t = 1812433253 * (MT[i-1] ^ (MT[i-1] >> 30)) + i;
MT[i] = t & 0xffffffff; //取最後的32位
}
}

梅森旋轉
void generate()
{
for(int i=0; i<624; i++)
{
// 2^31 = 0x80000000
// 2^31-1 = 0x7fffffff
int y = (MT[i] & 0x80000000) + (MT[(i+1) % 624] & 0x7fffffff);
MT[i] = MT[(i + 397) % 624] ^ (y >> 1);
if (y & 1)
MT[i] ^= 2567483615;
}
}

輸出函數
int rand()
{
if(!isInit)
srand((int)time(NULL));
if(index == 0)
generate();
int y = MT[index];
y = y ^ (y >> 11);
y = y ^ ((y << 7) & 2636928640);
y = y ^ ((y << 15) & 4022730752);
y = y ^ (y >> 18);
index = (index + 1) % 624;
return y; //筆者注：y即爲產生的隨機數
}

int main()
{
srand(0); //設置隨機種子
int cnt = 0;
for(int i=0; i<1000000; i++) //下面的循環是用來判斷隨機數的奇偶機率的
{
if(rand() & 1)
cnt++;
}
cout<<cnt / 10000.0<<"%"<<endl;
return 0;
}
```

->continue

# 填一下前面的坑

這裏回答一下前面的那個問題：

爲何循環節是2^n-1而不是2^n

這個問題的答案和爲何初始序列不能是 { 0 , 0 , 0 , 0 }是同樣的，由於若是全是0的話，不管怎麼異或運算都不能產生循環。那麼還怎麼僞隨機啊。

由於不能是全0，因此循環節要-1

最後很是感謝你能有耐心讀到這裏。

本文到這裏應該就 ~~水完~~ 結束了，固然，既然你好不容易看到了這裏，我就給一個彩蛋吧（ 有點勉強 ）。

關於rand函數爲何是用1103515245和12345這兩個數...你能夠理解爲玄學。 不過真是緣由是用這兩個數推算出來的的隨機數分佈相對平均。更符合僞隨機數的特性。（ 這個我盡力用實驗來論證，目前還在構思，也可能正在實驗 ）

感謝@[qbu666666](https://www.luogu.org/space/show?uid=157598)和@[dgklr](https://www.luogu.org/space/show?uid=157598)大佬對本文文字錯誤以及論述缺陷的指出。

而後特別感謝一下@[MZW_BG](https://www.luogu.org/space/show?uid=97504)對本文真隨機部分的提醒以及幫助。

你們都很強，可與之共勉。