machine learning[GMM-EM]

---

介紹下EM算法和GMM模型，先簡單介紹GMM的物理意義，而後給出最直接的迭代過程；而後再介紹EM。

1 高斯混合模型

高斯分佈，是統計學中的模型，其輸出值表示當前輸入數據樣本（一維標量，多維向量）的機率。

1.1 多元高斯分佈

如高斯分佈-筆記所述，多元高斯函數公式爲： $$p({\bf x})=\frac{1}{(2\pi)^{\frac{d}{2}}|\Sigma|^\frac{1}{2}}exp{-\frac{1}{2}({\bf x-\mu})^T{\Sigma}^{-1}({\bf x-\mu})} $$ 其中${\bf x}=[x_1,x_2,...,x_d]^T$是$d$維的列向量； ${\bf \mu}=[\mu_1,\mu_2,...,\mu_d]^T$是$d$維均值的列向量； $\Sigma$是$d\times d$維的協方差矩陣； ${\Sigma}^{-1}$是$\Sigma$的逆矩陣; $|\Sigma|$是$\Sigma$的行列式； $(\bf x-\mu)^T$是$(\bf x-\mu)$的轉置，且 $$\mu=E(\bf x) $$ $$\Sigma=E{(\bf x-\bf \mu)(\bf x - \mu)^T}$$ 其中$\mu,\Sigma$分別是向量$\bf x$和矩陣$(\bf x -\mu)(\bf x -\mu)^T$的指望。

1.1 高斯混合模型定義

如圖所示，假定咱們當前的樣本都是2維特徵的樣本，即表如今特徵空間中就是在2維座標系上有多個數據點

<center/>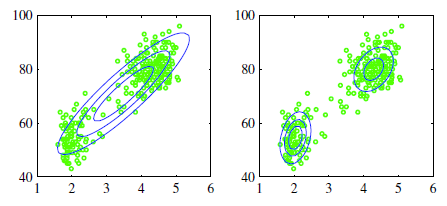</center> <center/>**圖1.1.1 二維空間中的數據樣本下，用一個高斯分佈去擬合，或者2個高斯分佈模型去擬合**</center> 從左圖可看出，經過一個高斯模型去擬合，總以爲很違和，由於所謂的高斯分佈是中間密集，而後隨着距離越遠則越稀疏，即**密集和稀疏程度就表示着當前出現樣本點的機率**,如 <center/>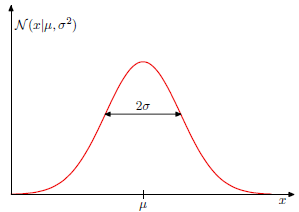</center> <center/>**圖1.1.2 一維高斯圖形,其中x軸表示輸入值，y軸表示機率值**</center> <center/></center> <center/>**圖 1.1.3二維高斯分佈呈現，乃至球面高斯分佈圖形。**</center> ps: **在最後一個圖形中，z軸表示當前出現樣本的機率，能夠看出越靠近中心，樣本出現的機率越大，而越遠離，則樣本出現的機率越小** 回頭看圖1.1.1，能夠得出，若是是這種數據，是不合適用單一高斯分佈去擬合的。

接下來咱們看看兩個例子：

• 假設paperback書籍的售價是服從均值爲10.00，標準差爲1.00的高斯分佈；而hardback 書籍的售價服從均值爲17，方差爲1.5的高斯分佈。那麼隨便挑一本書，其價格是服從單一高斯分佈麼？ 結果確定是否。直觀來講，單一高斯分佈是中間密度大，而離中間越遠則密度會快速降低就像單一山峯，可是這裏隨便挑一本的價格倒是服從雙峯的。這裏分佈的中心的售價大約是13，而找到13塊錢的一本書的機率卻遠低於10或者17的周邊。
• 另外一個例子：略

<center/>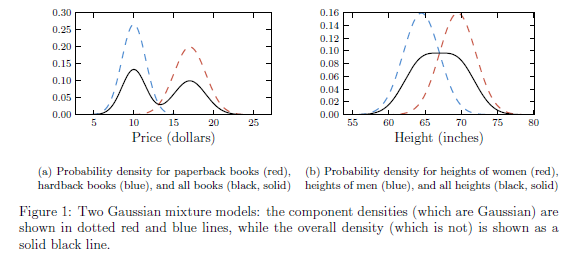</center> <center/>**圖1.1.4 一維數據下的高斯混合模型的兩個例子**</center> 這裏咱們先簡單拿出高斯混合模型的公式： <center/>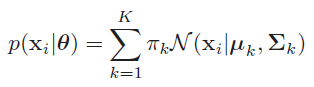</center> 如公式所述，所謂多維高斯分佈，就是多個高斯分佈的線性組合，也就是經過將多個高斯分佈乘以對應的權重來完成樣本數據的擬合。在這其中 $0 \leq \pi_k \geq 1$，且$\sum{\pi_k} =1$ 即，這裏表達的物理意義是： > * **在多維特徵空間中，每個樣本是基於多個高斯分佈而生成的，好比基於當前$\theta$基礎上，$p(x_i| \theta)=0.5*G1+0.3*G2+0.2*G1$** 意思就是該樣本點50%機率來自高斯1分佈，30%機率來自高斯2分佈，20%機率來自高斯3分佈。

上面介紹的都是2個高斯分佈的狀況，以下圖，假設咱們引入三個高斯分佈

<center/>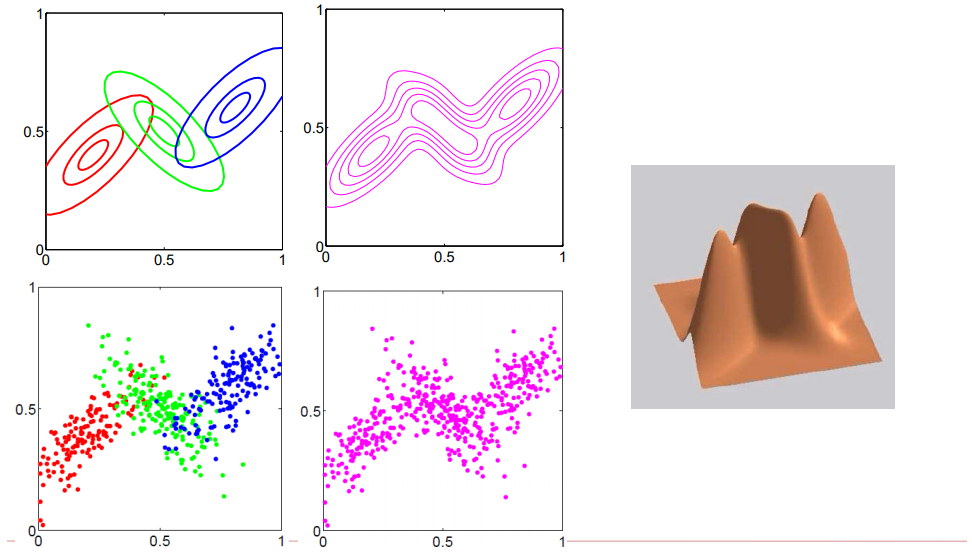</center> <center/>**圖1.1.5 三個高斯分佈在2維空間中的展現**</center> 如上圖所述，咱們拿到的樣本集合天然都是一些在特徵空間中的點，所謂用**混合高斯模型去擬合，也就是爲了求得每一個樣本點來自對應的高斯分佈的機率（$\pi_k$）以及每一個高斯分佈的參數（均值和方差）**。能夠天然推廣出，只要參與的高斯分佈越多，那麼就能表示越多的樣本點，那麼只要足夠多的高斯分佈進行線性組合，那麼就能擬合整個特徵維度的空間中表示的樣本。

1.2 求每一個樣本屬於不一樣高斯分佈的機率

如1.1中混合高斯的公式

<center/>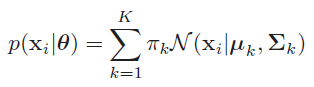</center> 咱們將其簡寫成 <center/>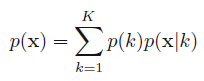</center> 這裏表示的就是每一個樣本的機率來自全部基於選定第$k$個高斯分佈基礎上該高斯分佈的機率之和。那麼對應的後驗機率$p(k|\mathbf{x})$咱們表示成$\gamma_k( \mathbf{x} )$: <center/>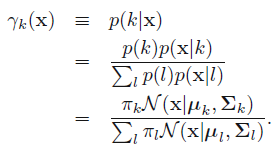</center> 對應的含義： > * **基於當前參數集合固定的基礎上，給定一個樣本，該樣原本自第k個高斯分佈的機率**，從而完成了先混合高斯聚類，而後進行簡單分類的過程。

1.3 用EM進行估計GMM的參數的直接過程

GMM模型如上述解釋的，如今，咱們關注點就到了如何去用GMM擬合樣本集，也就是訓練過程。這其中，K是須要預先人爲指定的，就和K-means同樣。那麼在指定了K以後，整個GMM模型的參數一共爲$\pi,\mu,\Sigma$.而一般用來訓練GMM的算法叫作EM算法，也就是(expectation maximization,EM) (Dempster et al. 1977; Meng and van Dyk 1997; McLachlan and Krishnan 1997)。下面會詳細介紹EM算法，而這裏爲了簡潔，就直接給出基於EM算法的GMM求解過程： 衆所周知，EM包含了兩個階段：

• E階段：求指望函數；
• M階段：對指望函數最大化。

在這其中，咱們須要計算最大似然估計，也就是,假設咱們有$N$個樣本，每一個樣本表示爲$\mathbf{x}_i$，且假設有$K$個高斯分佈，則對應的最大似然估計就是 $$p(\mathbf{X}|\pi, \mu, \Sigma)=\prod_n^{N} p(x_n|\pi, \mu, \Sigma)$$ 左右取對數得：

<center/>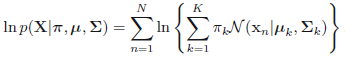</center>

而對於GMM模型來講，對應的階段爲：

• 初始化階段：先隨機初始化$\pi, \mu, \Sigma$ 。
• E階段：使用當前的參數，基於每一個樣本計算各自的高斯響應值(就是以前介紹的後驗機率$p(k|\mathbf{x})$)

<center/>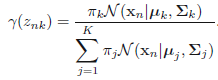</center> ps:**一共$N$個樣本，每一個樣本都有$K$次計算，則當前E階段一共須要計算$N \times K$次** > * M階段：更新參數，基於全部樣本，計算各自對應的高斯參數。**咱們能夠想象這樣一個網格，其中行表示$N$個樣本數量，列表示$K$個高斯模型，則E階段是計算網格全部的部分，而M階段是按照列，每次計算一列中$N$個值的均值，要計算$K$個模型次數**。 <center/>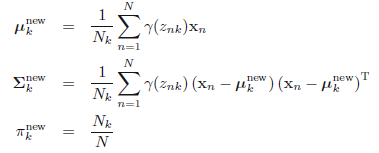</center> 這裏 <center/></center> > * 評估階段：計算log似然 <center/>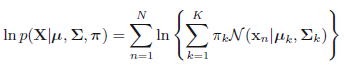</center> 並觀察log似然和參數$\pi, \mu, \Sigma$ 是否收斂，若是收斂則中止迭代，不然，接着計算E階段和M階段。

從上面能夠看出，基於EM的GMM計算須要的計算量有些大，故而若是樣本量較多，該方法一次迭代所須要的計算次數就不少。

2 EM算法

上面基於GMM給出了最終的簡潔結果，這裏咱們詳細介紹下EM的原理及概念。值得注意的是，EM算法對初始值十分敏感，且容易陷入局部最優。

2.1 EM通用計算流程

一般在ML中，給的數據無外乎樣本和標籤，若是咱們採用的模型是直接基於這些計算的，那麼就很容易了，好比k-means。而若是採用的模型是包含了隱含變量的，那麼對於整個算法來講，就還須要考慮到缺失的數據信息。也就是所謂的潛在變量。例如：

• 李航書裏面介紹的例子：有三個硬幣A，B，C。咱們先拋擲硬幣A，若是朝上則拋擲硬幣B，不然拋擲硬幣C。而後將硬幣B或者C的結果進行收集，看成觀測結果，那麼假設一共收集了十個[1,1,0,1,0,0,1,0,1,1]。但是咱們並不知道每次結果是來自B仍是來自C，其中包含着硬幣A的未觀測數據。因此咱們將觀測的結果視爲觀測變量，而硬幣A視爲潛在變量。
• GMM模型：給定一個樣本集合，其中每一個樣本點是觀測到的數據，而該數據來自哪一個高斯分佈是潛在變量（雖然$\pi_k$表示機率，但是咱們若是取最大機率的爲生成該樣本的高斯分佈，則能夠將其視爲one-hot形式）

EM算法就是一個迭代算法，經過E計算潛在變量的指望值；並在M階段基於潛在變量指望值去計算其餘模型變量的指望值。 咱們假設全部的觀測數據爲$\mathbf{X}={\mathbf{x}_1,\mathbf{x}_2,\mathbf{x}_3,...,\mathbf{x}_N}$，其中，該模型包含潛在變量$\mathbf{Z}={\mathbf{z}_1,\mathbf{z}_2,\mathbf{z}_3,...,\mathbf{z}_M}$,並假設全部的模型參數爲$\theta$,那麼該模型的log似然函數爲：

<center/>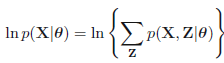</center> 等效於下面式子 <center/>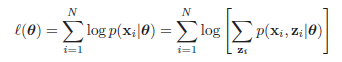</center> 其中$\mathbf{x}_i$表示在數據集中第$i$個觀測樣本，$\mathbf{z}_i$表示該觀測樣本下涉及的潛在變量，上式子中$p(\mathbf{x}_i|\theta)=\sum_{\mathbf{z}_i} p(\mathbf{x}_i,\mathbf{z}_i|\theta)$,即邊緣分佈。 從上面式子能夠看出log沒法更進一步的塞到求和操做裏面，而是先求和而後在log，而後再求和，這就致使計算十分困難。這裏咱們將$\{\mathbf{X},\mathbf{Z}\}$稱爲徹底數據，而將$\mathbf{X}$稱爲不徹底數據 。然而基於不徹底數據基礎上，咱們須要進行模型的參數迭代，因此咱們先要基於$\theta^{old}$計算$p(\mathbf{Z}|\mathbf{X},\theta^{old})$，而後計算$\theta^{new}$.

這裏一個重要函數$Q(\theta,\theta^{old})$（在M階段須要用到），其是基於給定觀測數據$\mathbf{X}$和當前參數$\theta^{old}$基礎上，對未觀測數據$\mathbf{Z}$的條件機率分佈$p(\mathbf{Z}|\mathbf{X},\theta^{old})$的指望（李航的觀點）.也能夠理解成基於給定觀測數據和當前參數基礎上對徹底數據的指望（mlapp觀點)。其中徹底數據的極大似然log函數爲$\log p(\mathbf{Z},\mathbf{X}|\theta)$

$$\begin{eqnarray} Q(\theta,\theta^{old}) &=& E_z [\log p(\mathbf{Z},\mathbf{X}|\theta)|\mathbf{X},\theta^{old} ] \ &=& \sum_\mathbf{Z} \log p(\mathbf{X}, \mathbf{Z} | \theta)p(\mathbf{Z} | \mathbf{X}, \theta^{old}) \ &=& \sum_{\mathbf{Z}}p(\mathbf{Z}|\mathbf{X},\theta^{old})\log p(\mathbf{X},\mathbf{Z}|\theta) \end{eqnarray}$$ ps：上式是示意式子，具體的過程能夠看基於GMM的EM過程更具體的瞭解這部分的變化。 通用EM流程爲：

• 初始化：先初始化參數$\theta^{old}$
• E階段：計算$p(\mathbf{Z}|\mathbf{X},\theta^{old})$
• M階段：計算$\theta^{new}=\underset{\theta}{argmax}Q(\theta,\theta^{old})$ 這裏$Q(\theta,\theta^{old})=\sum_{\mathbf{Z}}p(\mathbf{Z}|\mathbf{X},\theta^{old})\log p(\mathbf{X},\mathbf{Z}|\theta)$，所謂最大化也就是最大化$\sum_{\mathbf{Z}}log p(\mathbf{X},\mathbf{Z}|\theta)$這部分，即基於當前參數的徹底數據的指望
• 評估階段：檢查當前log似然函數和參數是否收斂，更換參數：$\theta^{old}=\theta^{new}$ 若是收斂則中止迭代，不然接着循環E階段和M階段

2.2 基於GMM的EM計算過程

這裏咱們從新回頭看GMM是如何用EM來求解的。 首先，假設觀測數據${\mathbf{x}_1,\mathbf{x}_2,...\mathbf{x}N}$是由高速混合模型生成的： $$p(\mathbf{X}|\theta)=\sum{k=1}^{K}\pi_k\phi(\mathbf{X}|\theta_k)$$ 其中，$\theta={\pi_1,\pi_2,...\pi_K;\theta_1,\theta_2,...\theta_K}$。

1 先明確潛在變量，寫出徹底數據的對數似然函數

這裏假設觀測數據$\mathbf{x}i$是這樣產生的：首先按照機率$\pi_k$選擇第k個高斯分佈，而後根據該高斯分佈生成該觀測數據。這時候，觀測數據$\mathbf{x}i$是已知的，而該觀測數據來自哪一個分佈是未知的，咱們假設爲$\gamma{jk}$,表示第$j$個樣本關於第$k$個高斯分佈的選擇： $$\gamma{jk}=\left{\begin{array}{cc} 1, & 第j個樣原本自第k個分模型\ 0, & other\ values \end{array}\right.$$ 其中$\gamma_{jk}$是個${0,1}$二值變量。 此時 基於每一個樣本的徹底數據是$(\mathbf{x}j,\gamma{j1},\gamma_{j2},...,\gamma_{jK})$,其中$j=1,2,...,N$ 則對應的徹底數據的似然函數爲： $$\begin{eqnarray}p(\mathbf{X},\mathbf{\gamma}|\theta) &=& \prod_{j=1}^{N}p(\mathbf{x}j,\gamma{j1},\gamma_{j2},...,\gamma_{jK}|\theta) \ &=& \prod_{k=1}^{K}\prod_{j=1}^{N}\left [\alpha_k \phi(\mathbf{x}j|\theta_k)\right ]^{\gamma{jk}}\ &=& \prod_{k=1}^K\alpha_k^{n_k}\prod_{j=1}^N\left [ \frac{1}{(2\pi)^{\frac{d}{2}}|\Sigma_k|^\frac{1}{2}}exp{-\frac{1}{2}({\mathbf{x}j-\mu_k})^T{\Sigma_k}^{-1}({\mathbf{x}j-\mu_k})}\right ]^{\gamma{jk}} \end{eqnarray}$$ 其中，$n_k=\sum{j=1}^N\gamma_{jk}$，$\sum_{k=1}^Kn_k=N$ 則，徹底數據的對數似然函數爲： $$\log p(\mathbf{X},\mathbf{\gamma}|\theta)=\sum_{k=1}^K n_k \log \alpha_k+\sum_{j=1}^N\gamma_{jk}\left [ \log\left(\frac{1}{(2\pi)^{\frac{d}{2}}}\right)-\log\left(\frac{1}{(|\Sigma_k|)^{\frac{1}{2}}}\right)-\frac{1}{2}({\mathbf{x}_j-\mu_k})^T{\Sigma_k}^{-1}({\mathbf{x}_j-\mu_k})\right ]$$

2 E階段，肯定Q函數

$$\begin{eqnarray}Q(\theta,\theta^{old}) &=& E\left [\log p(\mathbf{X},\mathbf{\gamma}|\theta)|\mathbf{X},\theta^{old}\right ]\ &=& E\left (\sum_{k=1}^K n_k \log \alpha_k+\sum_{j=1}^N\gamma_{jk}\left [\log\left(\frac{1}{(2\pi)^{\frac{d}{2}}}\right)-\log\left(\frac{1}{(|\Sigma_k|)^{\frac{1}{2}}}\right)-\frac{1}{2}({\mathbf{x}j-\mu_k})^T{\Sigma_k}^{-1}({\mathbf{x}j-\mu_k})\right ] \right ) \ &=& \sum{k=1}^K\left( \sum{j=1}^N(E\gamma_{jk})\log\alpha_k+\sum_{j=1}^N(E\gamma_{jk})\left [ \log\left(\frac{1}{(2\pi)^{\frac{d}{2}}}\right)-\log\left(\frac{1}{(|\Sigma_k|)^{\frac{1}{2}}}\right)-\frac{1}{2}({\mathbf{x}j-\mu_k})^T{\Sigma_k}^{-1}({\mathbf{x}j-\mu_k})\right ]\right)\ &=& \sum{k=1}^K\sum{j=1}^N(E\gamma_{jk})\left(\log\alpha_k+\left [ \log\left(\frac{1}{(2\pi)^{\frac{d}{2}}}\right)-\log\left(\frac{1}{(|\Sigma_k|)^{\frac{1}{2}}}\right)-\frac{1}{2}({\mathbf{x}j-\mu_k})^T{\Sigma_k}^{-1}({\mathbf{x}j-\mu_k})\right ]\right) \ \end{eqnarray}$$ ps:**最後一個式子，就等於2.1部分的表現形式$\sum{\mathbf{Z}}p(\mathbf{Z}|\mathbf{X},\theta^{old})\log p(\mathbf{X},\mathbf{Z}|\theta)$** 能夠看到，對整個徹底數據的指望，最後就須要求解關於潛在變量的指望，這裏只須要計算$E(\gamma{jk}|\mathbf{X},\theta)$,這裏記爲$\hat \gamma_{jk}$ 則 $$\begin{eqnarray}\hat \gamma_{jk} &=& E(\gamma_{jk}|\mathbf{X},\theta^{old})=p(\gamma_{jk}=1|\mathbf{X},\theta^{old})\ &=& \frac{p(\gamma_{jk}=1,\mathbf{x}j|\theta^{old})}{\sum{k=1}^Kp(\gamma_{jk}=1,\mathbf{x}j|\theta^{old})}\ &=& \frac{p(\gamma{jk}=1,\mathbf{x}j|\theta)p(\gamma{jk}=1|\theta)}{\sum_{k=1}^Kp(\gamma_{jk}=1,\mathbf{x}j|\theta)p(\gamma{jk}=1|\theta)}\ &=& \frac{\alpha_k\phi(\mathbf{x}j|\theta_k)}{\sum{k=1}^K\alpha_k\phi(\mathbf{x}j|\theta_k)} \end{eqnarray}$$ 其中$j=1,2,...,N;k=1,2,...K$。 將$\hat \gamma{jk}=E(\gamma_{jk}|\mathbf{X},\theta)$和$n_k=\sum_{j=1}^NE\hat \gamma_{jk}=\sum_{j=1}^N\gamma_{jk}$帶入得： $$Q(\theta,\theta^{old})=\sum_{k=1}^K n_k \log \alpha_k+\sum_{j=1}^N\hat \gamma_{jk}\left [ \log\left(\frac{1}{(2\pi)^{\frac{d}{2}}}\right)-\log\left(\frac{1}{(|\Sigma_k|)^{\frac{1}{2}}}\right)-\frac{1}{2}({\mathbf{x}_j-\mu_k})^T{\Sigma_k}^{-1}({\mathbf{x}_j-\mu_k})\right ] \ $$ ps:值得注意的是，上面式子中的中括號部分，能夠替換成任意其餘分模型，不必定是高斯模型

3 肯定M階段

M階段就是爲了求$Q(\theta,\theta^{old})$的關於$\theta$的極大值，即： $$\theta^{new}=\underset{\theta}{argmax}Q(\theta,\theta^{old})$$ 這裏用$\hat \mu_k$,$\hat \sigma_k^2$,$\hat \alpha_k$,$k=1,2,3,...,K$表示$\theta^{new}$中的各參數，求$\hat \mu_k$,$\hat \sigma_k^2$只須要將$Q(\theta,\theta^{old})$求偏導數，而後等於0，求出其值便可，而在求$\hat \alpha_k$時，由於有約束條件$\sum_{k=1}^K\alpha_k=1$，因此須要用拉格朗日乘子法求偏導。 $$\begin{eqnarray}\frac{dQ}{d\mu_k} &=& \sum_{j=1}^K\hat \gamma_{jk}\left[\Sigma_k(\mathbf{x}j-\mu_k)\right]\ \end{eqnarray}$$ 令其等於0，並左右乘以$\Sigma_k^{-1}$(咱們假設該協方差矩陣是非奇異的)。則$\sum{j=1}^N\hat \gamma_{jk}\mathbf{x}j=\sum{j=1}^N\hat \gamma_{jk}\mu_k=E\mu_k\sum_{j=1}^N\hat \gamma_{jk}$,因此 $$\hat \mu_k=\frac{\sum_{j=1}^N\hat \gamma_{jk}\mathbf{x}j}{\sum{j=1}^N\hat \gamma_{jk}}$$ 同理： $$\frac{dQ}{d\Sigma_k}=$$

2.3 EM的證實過程 李航

參考文獻：

• 高斯分佈-筆記
• Gaussian mixture models and the EM algorithm
• gmm
• Pattern.Recognition.and.Machine.Learning,.Christopher.M..Bishop,.Springer,.2006
• Machine learning a probabilistic perspective
• 李航統計學習方法
• 高斯混合模型（GMM）及其EM算法的理解
• matrix_cookbook
• Matrix_calculus